Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-13T08:26:36.178Z Has data issue: false hasContentIssue false
  • English
  • Français

On local aspects of topological weak mixing, sequence entropy and chaos

Published online by Cambridge University Press:  11 April 2013

PIOTR OPROCHA  and
GUOHUA ZHANG
PIOTR OPROCHA
Affiliation:
AGH University of Science and Technology, Faculty of Applied Mathematics, al. A. Mickiewicza 30, 30-059 Kraków, Poland email [email protected] Institute of Mathematics, Polish Academy of Sciences, ul. Śniadeckich 8, 00-956 Warszawa, Poland
GUOHUA ZHANG
Affiliation:
School of Mathematical Sciences and LMNS, Fudan University, Shanghai 200433, China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we show that for every 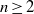$n\geq 2$ there are minimal systems with perfect weakly mixing sets of order $n$ and all weakly mixing sets of order 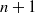$n+ 1$ trivial. We present some relations between weakly mixing sets and topological sequence entropy; in particular, we prove that invertible minimal systems with non-trivial weakly mixing sets of order three always have positive topological sequence entropy. We also study relations between weak mixing of sets and other well-established notions from qualitative theory of dynamical systems like (regional) proximality, chaos and equicontinuity in a broad sense.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 5 , October 2014 , pp. 1615 - 1639
Copyright
Copyright ©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alsedà, Ll., del Río, M. A. and Rodríguez, J. A.. Transitivity and dense periodicity for graph maps. J. Difference Equ. Appl. 9 (6) (2003), 577–598.CrossRefGoogle Scholar
Akin, E. and Glasner, E.. Residual properties and almost equicontinuity. J. Anal. Math. 84 (2001), 243–286.Google Scholar
Akin, E., Glasner, E., Huang, W., Shao, S. and Ye, X.. Sufficient conditions under which a transitive system is chaotic. Ergod. Th. & Dynam. Sys. 30 (2010), 1277–1310.Google Scholar
Akin, E. and Kolyada, S.. Li-Yorke sensitivity. Nonlinearity 16 (2003), 1421–1433.CrossRefGoogle Scholar
Blanchard, F.. Fully positive topological entropy and topological mixing. Symbolic Dynamics and its Applications (New Haven, CT, 1991) (Contemporary Mathematics, 135). American Mathematical Society, Providence, RI, 1992, pp. 95–105.Google Scholar
Blanchard, F.. A disjointness theorem involving topological entropy. Bull. Soc. Math. France 121 (4) (1993), 465–478.CrossRefGoogle Scholar
Blanchard, F., Host, B. and Maass, A.. Topological complexity. Ergod. Th. & Dynam. Sys. 20 (3) (2000), 641–662.CrossRefGoogle Scholar
Blanchard, F. and Huang, W.. Entropy sets, weakly mixing sets and entropy capacity. Discrete Contin. Dyn. Syst. 20 (2) (2008), 275–311.Google Scholar
Blanchard, F. and Kwiatkowski, J.. Minimal self-joinings and positive topological entropy. II. Studia Math. 128 (2) (1998), 121–133.Google Scholar
Coven, E. and Keane, M.. The structure of substitution minimal sets. Trans. Amer. Math. Soc. 162 (1971), 89–102.Google Scholar
Glasner, E.. Topological weak mixing and quasi-Bohr systems. Israel J. Math. 148 (2005), 277–304.CrossRefGoogle Scholar
Glasner, E. and Maon, D.. Rigidity in topological dynamics. Ergod. Th. & Dynam. Sys. 9 (2) (1989), 309–320.Google Scholar
Glasner, E. and Weiss, B.. On the construction of minimal skew products. Israel J. Math. 34 (4) (1979), 321–336.CrossRefGoogle Scholar
Glasner, E. and Weiss, B.. Sensitive dependence on initial conditions. Nonlinearity 6 (6) (1993), 1067–1075.Google Scholar
Glasner, E. and Weiss, B.. Locally equicontinuous dynamical systems. Colloq. Math. 84/85 (2000), 345–361.CrossRefGoogle Scholar
Glasner, E. and Ye, X.. Local entropy theory. Ergod. Th. & Dynam. Sys. 29 (2) (2009), 321–356.Google Scholar
Goodman, T. N. T.. Topological sequence entropy. Proc. Lond. Math. Soc. (3) 29 (1974), 331–350.CrossRefGoogle Scholar
Hahn, F. and Katznelson, Y.. On the entropy of uniquely ergodic transformations. Trans. Amer. Math. Soc. 126 (1967), 335–360.Google Scholar
Huang, W., Li, S. M., Shao, S. and Ye, X.. Null systems and sequence entropy pairs. Ergod. Th. & Dynam. Sys. 23 (5) (2003), 1505–1523.CrossRefGoogle Scholar
Llibre, J. and Misiurewicz, M.. Horseshoes, entropy and periods for graph maps. Topology 32 (1993), 649–664.Google Scholar
Maass, A. and Shao, S.. Structure of bounded topological-sequence-entropy minimal systems. J. Lond. Math. Soc. (2) 76 (3) (2007), 702–718.Google Scholar
Munkres, J. R.. Topology, 2nd edn. Prentice Hall, Upper Sadle River, NJ, 2000.Google Scholar
Oprocha, P.. Coherent lists and chaotic sets. Discrete Contin. Dyn. Syst. 31 (2011), 797–825.Google Scholar
Oprocha, P. and Zhang, G. H.. On local aspects of topological weak mixing in dimension one and beyond. Studia Math. 202 (2011), 261–288.CrossRefGoogle Scholar
Oprocha, P. and Zhang, G. H.. On sets with recurrence properties, their topological structure and entropy. Topology Appl. 159 (7) (2012), 1767–1777.Google Scholar
Oprocha, P. and Zhang, G. H.. Topological aspects of dynamics of pairs, tuples and sets, in Recent Progress in General Topology III, to appear.Google Scholar
Pavlov, R.. Some counterexamples in topological dynamics. Ergod. Th. & Dynam. Sys. 28 (2008), 1291–1322.Google Scholar
Petersen, K. E.. A topologically strongly mixing symbolic minimal set. Trans. Amer. Math. Soc. 148 (1970), 603–612.CrossRefGoogle Scholar
Tan, F.. The set of sequence entropies for graph maps. Topology Appl. 158 (3) (2011), 533–541.Google Scholar
Tan, F., Ye, X. and Zhang, R. F.. The set of sequence entropies for a given space. Nonlinearity 23 (1) (2010), 159–178.Google Scholar
Zhang, G. H.. Relativization of complexity and sensitivity. Ergod. Th. & Dynam. Sys. 27 (4) (2007), 1349–1371.Google Scholar
Zhang, G. H.. Relativization of dynamical properties. Sci. China Math. 55 (5) (2012), 913–936.Google Scholar