Published online by Cambridge University Press: 21 July 2015
We provide a new proof of a theorem whose proof was sketched by Sullivan [Disjoint spheres, approximation by imaginary quadratic numbers, and the logarithm law for geodesics. Acta Math.149(3–4) (1982), 215–237], namely that if the Poincaré exponent of a geometrically finite Kleinian group 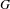 $G$ is strictly between its minimal and maximal cusp ranks, then the Patterson–Sullivan measure of
$G$ is strictly between its minimal and maximal cusp ranks, then the Patterson–Sullivan measure of 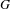 $G$ is not proportional to the Hausdorff or packing measure of any gauge function. This disproves a conjecture of Stratmann [Multiple fractal aspects of conformal measures; a survey. Workshop on Fractals and Dynamics (Mathematica Gottingensis, 5). Eds. M. Denker, S.-M. Heinemann and B. Stratmann. Springer, Berlin, 1997, pp. 65–71; Fractal geometry on hyperbolic manifolds. Non-Euclidean Geometries (Mathematical Applications (N.Y.), 581). Springer, New York, 2006, pp. 227–247].
$G$ is not proportional to the Hausdorff or packing measure of any gauge function. This disproves a conjecture of Stratmann [Multiple fractal aspects of conformal measures; a survey. Workshop on Fractals and Dynamics (Mathematica Gottingensis, 5). Eds. M. Denker, S.-M. Heinemann and B. Stratmann. Springer, Berlin, 1997, pp. 65–71; Fractal geometry on hyperbolic manifolds. Non-Euclidean Geometries (Mathematical Applications (N.Y.), 581). Springer, New York, 2006, pp. 227–247].