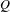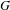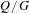Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de Paula Ramos, Gustavo
2024.
Multiplicity of solutions to a nonlinear elliptic problem on a Riemannian orbifold.
Nonlinear Analysis,
Vol. 238,
Issue. ,
p.
113387.