No CrossRef data available.
Published online by Cambridge University Press: 03 April 2017
The canonical unitary representation of a locally compact separable group arising from an ergodic action of the group on a von Neumann algebra with separable predual preserving a faithful normal semifinite (infinite) weight is weak mixing. On the contrary, there exists a non-ergodic automorphism of a von Neumann algebra preserving a faithful normal semifinite trace such that the spectral measure and the spectral multiplicity of the induced action are respectively the Haar measure (on the unit circle) and 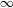 $\infty$. Despite not even being ergodic, this automorphism has the same spectral data as that of a Bernoulli shift.
$\infty$. Despite not even being ergodic, this automorphism has the same spectral data as that of a Bernoulli shift.