Published online by Cambridge University Press: 20 September 2022
We prove that for any non-degenerate dendrite D, there exist topologically mixing maps 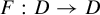 $F : D \to D$ and
$F : D \to D$ and 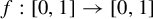 $f : [0, 1] \to [0, 1]$ such that the natural extensions (as known as shift homeomorphisms)
$f : [0, 1] \to [0, 1]$ such that the natural extensions (as known as shift homeomorphisms) 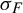 $\sigma _F$ and
$\sigma _F$ and 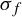 $\sigma _f$ are conjugate, and consequently the corresponding inverse limits are homeomorphic. Moreover, the map f does not depend on the dendrite D and can be selected so that the inverse limit
$\sigma _f$ are conjugate, and consequently the corresponding inverse limits are homeomorphic. Moreover, the map f does not depend on the dendrite D and can be selected so that the inverse limit 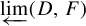 $\underleftarrow {\lim } (D,F)$ is homeomorphic to the pseudo-arc. The result extends to any finite number of dendrites. Our work is motivated by, but independent of, the recent result of the first and third author on conjugation of Lozi and Hénon maps to natural extensions of dendrite maps.
$\underleftarrow {\lim } (D,F)$ is homeomorphic to the pseudo-arc. The result extends to any finite number of dendrites. Our work is motivated by, but independent of, the recent result of the first and third author on conjugation of Lozi and Hénon maps to natural extensions of dendrite maps.