Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Salo, Ville
2015.
Cellular Automata and Discrete Complex Systems.
Vol. 9099,
Issue. ,
p.
17.
Kra, Bryna
and
Cyr, Van
2016.
The automorphism group of a minimal shift of stretched exponential growth.
Journal of Modern Dynamics,
Vol. 10,
Issue. 02,
p.
483.
Baake, Michael
A. G. Roberts, John
and
Yassawi, Reem
2018.
Reversing and extended symmetries of shift spaces.
Discrete & Continuous Dynamical Systems - A,
Vol. 38,
Issue. 2,
p.
835.
Medynets, Kostya
and
Talisse, James P.
2019.
Toeplitz subshifts with trivial centralizers and positive entropy.
Involve, a Journal of Mathematics,
Vol. 12,
Issue. 3,
p.
395.
BERTHÉ, VALÉRIE
STEINER, WOLFGANG
THUSWALDNER, JÖRG M.
and
YASSAWI, REEM
2019.
Recognizability for sequences of morphisms.
Ergodic Theory and Dynamical Systems,
Vol. 39,
Issue. 11,
p.
2896.
SALO, VILLE
2019.
Transitive action on finite points of a full shift and a finitary Ryan’s theorem.
Ergodic Theory and Dynamical Systems,
Vol. 39,
Issue. 06,
p.
1637.
FRISCH, JOSHUA
SCHLANK, TOMER
and
TAMUZ, OMER
2019.
Normal amenable subgroups of the automorphism group of the full shift.
Ergodic Theory and Dynamical Systems,
Vol. 39,
Issue. 5,
p.
1290.
Guillon, Pierre
Jeandel, Emmanuel
Kari, Jarkko
and
Vanier, Pascal
2019.
Computer Science – Theory and Applications.
Vol. 11532,
Issue. ,
p.
180.
Dolce, Francesco
and
Perrin, Dominique
2019.
Computer Science – Theory and Applications.
Vol. 11532,
Issue. ,
p.
106.
CYR, VAN
and
KRA, BRYNA
2020.
The automorphism group of a shift of slow growth is amenable.
Ergodic Theory and Dynamical Systems,
Vol. 40,
Issue. 7,
p.
1788.
SCHMIEDING, SCOTT
2020.
Automorphisms of the shift: Lyapunov exponents, entropy, and the dimension representation.
Ergodic Theory and Dynamical Systems,
Vol. 40,
Issue. 9,
p.
2552.
DOLCE, FRANCESCO
and
PERRIN, DOMINIQUE
2021.
Eventually dendric shift spaces.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 7,
p.
2023.
Donoso, Sebastián
Durand, Fabien
Maass, Alejandro
and
Petite, Samuel
2021.
Interplay between finite topological rank minimal Cantor systems, 𝒮-adic subshifts and their complexity.
Transactions of the American Mathematical Society,
Vol. 374,
Issue. 5,
p.
3453.
Cortez, Marìa Isabel
2021.
2019-20 MATRIX Annals.
Vol. 4,
Issue. ,
p.
679.
BAAKE, M.
BUSTOS, Á.
HUCK, C.
LEMAŃCZYK, M.
and
NICKEL, A.
2021.
Number-theoretic positive entropy shifts with small centralizer and large normalizer.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 11,
p.
3201.
Cyr, Van
Johnson, Aimee
Kra, Bryna
and
Şahİn, Ayşe
2022.
The complexity threshold for the emergence of Kakutani inequivalence.
Israel Journal of Mathematics,
Vol. 251,
Issue. 1,
p.
271.
ZUCKER, ANDY
2022.
Minimal flows with arbitrary centralizer.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 1,
p.
310.
ESPINOZA, BASTIÁN
and
MAASS, ALEJANDRO
2022.
On the automorphism group of minimal -adic subshifts of finite alphabet rank.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 9,
p.
2800.
Hartman, Yair
Kra, Bryna
and
Schmieding, Scott
2022.
The Stabilized Automorphism Group of a Subshift.
International Mathematics Research Notices,
Vol. 2022,
Issue. 21,
p.
17112.
Keller, Gerhard
Lemańczyk, Mariusz
Richard, Christoph
and
Sell, Daniel
2022.
On the Garden of Eden theorem for ℬ-free subshifts.
Israel Journal of Mathematics,
Vol. 251,
Issue. 2,
p.
567.
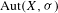 $\text{Aut}(X,{\it\sigma})$ of subshifts
$\text{Aut}(X,{\it\sigma})$ of subshifts 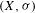 $(X,{\it\sigma})$ of low word complexity. In particular, we prove that
$(X,{\it\sigma})$ of low word complexity. In particular, we prove that 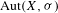 $\text{Aut}(X,{\it\sigma})$ is virtually
$\text{Aut}(X,{\it\sigma})$ is virtually  $\mathbb{Z}$ for aperiodic minimal subshifts and certain transitive subshifts with non-superlinear complexity. More precisely, the quotient of this group relative to the one generated by the shift map is a finite group. In addition, we show that any finite group can be obtained in this way. The class considered includes minimal subshifts induced by substitutions, linearly recurrent subshifts and even some subshifts which simultaneously exhibit non-superlinear and superpolynomial complexity along different subsequences. The main technique in this article relies on the study of classical relations among points used in topological dynamics, in particular, asymptotic pairs. Various examples that illustrate the technique developed in this article are provided. In particular, we prove that the group of automorphisms of a
$\mathbb{Z}$ for aperiodic minimal subshifts and certain transitive subshifts with non-superlinear complexity. More precisely, the quotient of this group relative to the one generated by the shift map is a finite group. In addition, we show that any finite group can be obtained in this way. The class considered includes minimal subshifts induced by substitutions, linearly recurrent subshifts and even some subshifts which simultaneously exhibit non-superlinear and superpolynomial complexity along different subsequences. The main technique in this article relies on the study of classical relations among points used in topological dynamics, in particular, asymptotic pairs. Various examples that illustrate the technique developed in this article are provided. In particular, we prove that the group of automorphisms of a 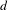 $d$-step nilsystem is nilpotent of order
$d$-step nilsystem is nilpotent of order 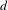 $d$ and from there we produce minimal subshifts of arbitrarily large polynomial complexity whose automorphism groups are also virtually
$d$ and from there we produce minimal subshifts of arbitrarily large polynomial complexity whose automorphism groups are also virtually  $\mathbb{Z}$.
$\mathbb{Z}$.