Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:44:11.507Z Has data issue: false hasContentIssue false
  • English
  • Français

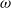$\omega $-recurrence in skew products

Published online by Cambridge University Press:  03 April 2013

JON CHAIKA  and
DAVID RALSTON
JON CHAIKA
Affiliation:
Department of Mathematics, University of Chicago, 5734 S. University Avenue, Chicago, IL 60637, USA email [email protected]
DAVID RALSTON
Affiliation:
Depatment of Mathematics/CIS, SUNY College at Old Westbury, PO 210, Old Westbury, NY 11568, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The rate of recurrence to measurable subsets in a conservative, ergodic infinite-measure-preserving system is quantified by generic divergence or convergence of certain sums given by a function 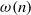$\omega (n)$. In the context of skew products over transformations of a probability space, we relate this notion to the more frequently studied question of the growth rate of ergodic sums (including Lyapunov exponents). We study in particular skew products over an irrational rotation given by bounded variation 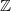$ \mathbb{Z} $-valued functions: first the generic situation is studied and recurrence quantified, and then certain specific skew products over rotations are shown to violate this generic rate of recurrence.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 5 , October 2014 , pp. 1525 - 1537
Copyright
Copyright ©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Conze, J.-P. and Frączek, K.. Cocycles over interval exchange transformations and multivalued Hamiltonian flows. Adv. Math. 226 (5) (2011), 4373–4428.CrossRefGoogle Scholar
Conze, J.-P.. Recurrence, ergodicity and invariant measures for cocycles over a rotation. Contemp. Math. 485 (2009), 45–70.Google Scholar
Khintchine, A.. Metrische Kettenbruchprobleme. Compositio Math. 1 (1935), 361–382.Google Scholar
Krengel, U.. Classification of states for operators. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Vol. 2. Eds. LeCam, L. and Neyman, J.. University of California Press, Berkeley, 1967, pp. 415–429.Google Scholar
Ralston, D.. Substitutions and $1/ 2$-discrepancy sums of $\{ n\theta + x\} $. Acta Arith. 154 (1) (2012), 1–28.Google Scholar
Viana, M.. Ergodic theory of interval exchange maps. Rev. Mat. Complut. 19 (1) (2006), 7–100.Google Scholar