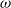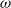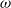Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
BARWELL, ANDREW D.
MEDDAUGH, JONATHAN
and
RAINES, BRIAN E.
2015.
Shadowing and -limit sets of circular Julia sets.
Ergodic Theory and Dynamical Systems,
Vol. 35,
Issue. 4,
p.
1045.
Averbeck, Nathan
and
Raines, Brian E.
2015.
Distributional chaos in dendritic and circular Julia sets.
Journal of Mathematical Analysis and Applications,
Vol. 428,
Issue. 2,
p.
951.
GOOD, CHRIS
and
MEDDAUGH, JONATHAN
2018.
Orbital shadowing, internal chain transitivity and -limit sets.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 1,
p.
143.
Brian, Will
and
Oprocha, Piotr
2018.
Ultrafilters and Ramsey-type shadowing phenomena in topological dynamics.
Israel Journal of Mathematics,
Vol. 227,
Issue. 1,
p.
423.
Meddaugh, Jonathan
and
Raines, Brian E.
2019.
Weak specification and Baire Space.
Journal of Mathematical Analysis and Applications,
Vol. 479,
Issue. 1,
p.
1355.
Good, Chris
Mitchell, Joel
and
Thomas, Joe
2020.
Preservation of shadowing in discrete dynamical systems.
Journal of Mathematical Analysis and Applications,
Vol. 485,
Issue. 1,
p.
123767.
Good, Chris
Mitchell, Joel
and
Thomas, Joe
2020.
On inverse shadowing.
Dynamical Systems,
Vol. 35,
Issue. 3,
p.
539.
Good, Chris
Meddaugh, Jonathan
and
Mitchell, Joel
2020.
Shadowing, internal chain transitivity and α-limit sets.
Journal of Mathematical Analysis and Applications,
Vol. 491,
Issue. 1,
p.
124291.
Meddaugh, Jonathan
and
Raines, Brian E.
2021.
A characterization of ω-limit sets in subshifts of Baire space.
Journal of Mathematical Analysis and Applications,
Vol. 500,
Issue. 1,
p.
125097.