Article contents
The number of ergodic measures for transitive subshifts under the regular bispecial condition
Published online by Cambridge University Press: 29 December 2020
Abstract
If 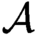 $\mathcal {A}$
is a finite set (alphabet), the shift dynamical system consists of the space
$\mathcal {A}$
is a finite set (alphabet), the shift dynamical system consists of the space 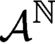 $\mathcal {A}^{\mathbb {N}}$
of sequences with entries in
$\mathcal {A}^{\mathbb {N}}$
of sequences with entries in 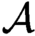 $\mathcal {A}$
, along with the left shift operator S. Closed S-invariant subsets are called subshifts and arise naturally as encodings of other systems. In this paper, we study the number of ergodic measures for transitive subshifts under a condition (‘regular bispecial condition’) on the possible extensions of words in the associated language. Our main result shows that under this condition, the subshift can support at most
$\mathcal {A}$
, along with the left shift operator S. Closed S-invariant subsets are called subshifts and arise naturally as encodings of other systems. In this paper, we study the number of ergodic measures for transitive subshifts under a condition (‘regular bispecial condition’) on the possible extensions of words in the associated language. Our main result shows that under this condition, the subshift can support at most 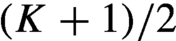 $({K+1})/{2}$
ergodic measures, where K is the limiting value of
$({K+1})/{2}$
ergodic measures, where K is the limiting value of 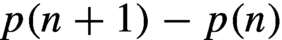 $p(n+1)-p(n)$
, and p is the complexity function of the language. As a consequence, we answer a question of Boshernitzan from 1984, providing a combinatorial proof for the bound on the number of ergodic measures for interval exchange transformations.
$p(n+1)-p(n)$
, and p is the complexity function of the language. As a consequence, we answer a question of Boshernitzan from 1984, providing a combinatorial proof for the bound on the number of ergodic measures for interval exchange transformations.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
Footnotes
This paper is dedicated to Michael Boshernitzan, whose enthusiasm and passion remain an inspiration for mathematicians, both present and future.
References
REFERENCES
- 8
- Cited by



