Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T00:41:59.903Z Has data issue: false hasContentIssue false
  • English
  • Français

Norm convergence of continuous-time polynomial multiple ergodic averages

Published online by Cambridge University Press:  21 October 2011

TIM AUSTIN
TIM AUSTIN*
Affiliation:
Department of Mathematics, Brown University, Box 1917, 151 Thayer Street, Providence, RI 02912, USA (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For a jointly measurable probability-preserving action τ:ℝD↷(X,μ) and a tuple of polynomial maps pi:ℝ→ℝD, i=1,2,…,k, the multiple ergodic averages 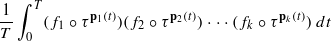converge in L2(μ) as T→∞ for any f1,f2,…,fk∈L∞(μ). This confirms the continuous-time analog of the conjectured norm convergence of discrete polynomial multiple ergodic averages, which in its original formulation remains open in most cases. A proof of convergence can be given based on the idea of passing up to a sated extension of (X,μ,τ) in order to find a simple partially characteristic factor, similarly to the recent development of this idea for the study of related discrete-time averages, together with a new inductive scheme on tuples of polynomials. The new induction scheme becomes available upon changing the time variable in the above integral by some fractional power, and provides an alternative to Bergelson’s polynomial ergodic theorem induction, which has been the mainstay of positive results in this area in the past.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 32 , Issue 2: Daniel J. Rudolph – in Memoriam , April 2012 , pp. 361 - 382
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Austin, T.. Deducing the multidimensional Szemerédi theorem from an infinitary removal lemma. J. Anal. Math. 111 (2010), 131–150.Google Scholar
[2]Austin, T.. Pleasant extensions retaining algebraic structure, I. Preprint, available online at arXiv.org:0905.0518.Google Scholar
[3]Austin, T.. Pleasant extensions retaining algebraic structure, II. Preprint, available online at arXiv.org:0910.0907.Google Scholar
[4]Austin, T.. On the norm convergence of nonconventional ergodic averages. Ergod. Th. & Dynam. Sys. 30(2) (2009), 321–338.CrossRefGoogle Scholar
[5]Bergelson, V.. Weakly mixing PET. Ergod. Th. & Dynam. Sys. 7(3) (1987), 337–349.Google Scholar
[6]Bergelson, V.. Ergodic Ramsey theory – an update. Ergodic Theory of ℤd-actions: Proceedings of the Warwick Symposium 1993–4. Eds. Pollicott, M. and Schmidt, K.. Cambridge University Press, Cambridge, 1996, pp. 1–61.Google Scholar
[7]Bergelson, V. and Knutson, I.. Weak mixing implies weak mixing of higher orders along tempered functions. Ergod. Th. & Dynam. Sys. 29(5) (2009), 1375–1416.Google Scholar
[8]Bergelson, V. and Leibman, A.. A nilpotent Roth theorem. Invent. Math. 147(2) (2002), 429–470.Google Scholar
[9]Bergelson, V., Leibman, A. and Moreira, C.. From discrete- to continuous-time ergodic theorems. Preprint, 2010.CrossRefGoogle Scholar
[10]Chu, Q.. Convergence of weighted polynomial multiple ergodic averages. Proc. Amer. Math. Soc. 137 (2009), 1363–1369.Google Scholar
[11]Chu, Q., Frantzikinakis, N. and Host, B.. Ergodic averages of commuting transformations with distinct degree polynomial iterates. Proc. Lond. Math. Soc. 102(5) (2011), 801–842.Google Scholar
[12]Conze, J.-P. and Lesigne, E.. Théorèmes ergodiques pour des mesures diagonales. Bull. Soc. Math. France 112(2) (1984), 143–175.Google Scholar
[13]Conze, J.-P. and Lesigne, E.. Sur un théorème ergodique pour des mesures diagonales. Probabilités (Publications de l’Institut de Recherche Mathématique de Rennes, 1987). University of Rennes I, Rennes, 1988, pp. 1–31.Google Scholar
[14]Conze, J.-P. and Lesigne, E.. Sur un théorème ergodique pour des mesures diagonales. C. R. Acad. Sci. Paris Sér. I Math. 306(12) (1988), 491–493.Google Scholar
[15]Frantzikinakis, N. and Kra, B.. Convergence of multiple ergodic averages for some commuting transformations. Ergod. Th. & Dynam. Sys. 25(3) (2005), 799–809.CrossRefGoogle Scholar
[16]Furstenberg, H.. Ergodic behaviour of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.Google Scholar
[17]Furstenberg, H. and Katznelson, Y.. An ergodic Szemerédi theorem for commuting transformations. J. Anal. Math. 34 (1978), 275–291.Google Scholar
[18]Furstenberg, H. and Weiss, B.. A mean ergodic theorem for . Convergence in Ergodic Theory and Probability. Eds. Bergleson, V. and Rosenblatt, A.. De Gruyter, Berlin, 1996, pp. 193–227.Google Scholar
[19]Host, B.. Ergodic seminorms for commuting transformations and applications. Studia Math. 195(1) (2009), 31–49.Google Scholar
[20]Host, B. and Kra, B.. Convergence of Conze–Lesigne averages. Ergod. Th. & Dynam. Sys. 21(2) (2001), 493–509.Google Scholar
[21]Host, B. and Kra, B.. Convergence of polynomial ergodic averages. Israel J. Math. 149 (2005), 1–19.CrossRefGoogle Scholar
[22]Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161(1) (2005), 397–488.Google Scholar
[23]Johnson, M. C. R.. Convergence of polynomial ergodic averages of several variables for some commuting transformations. Illinois J. Math. 53(3) (2009), 865–882.Google Scholar
[24]Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences (Pure and Applied Mathematics). Wiley-Interscience (John Wiley), New York, 1974.Google Scholar
[25]Leibman, A.. Multiple recurrence theorem for measure preserving actions of a nilpotent group. Geom. Funct. Anal. 8(5) (1998), 853–931.Google Scholar
[26]Leibman, A.. Convergence of multiple ergodic averages along polynomials of several variables. Israel J. Math. 146 (2005), 303–315.Google Scholar
[27]Potts, A.. Multiple ergodic averages for flows and an application. Preprint, 2009, available online at arXiv.org:0910.3687, Illinois J. Math. to appear.Google Scholar
[28]Rudolph, D. J.. Eigenfunctions of T×S and the Conze–Lesigne algebra. Ergodic Theory and its Connections with Harmonic Analysis (Alexandria, 1993) (London Mathematical Society Lecture Note Series, 205). Cambridge University Press, Cambridge, 1995, pp. 369–432.Google Scholar
[29]Tao, T.. Norm convergence of multiple ergodic averages for commuting transformations. Ergod. Th. & Dynam. Sys. 28 (2008), 657–688.Google Scholar
[30]Zhang, Q.. On convergence of the averages (1/N)∑ Nn=1f 1(R nx)f 2(S nx)f 3(T nx). Monatsh. Math. 122(3) (1996), 275–300.Google Scholar
[31]Ziegler, T.. Universal characteristic factors and Furstenberg averages. J. Amer. Math. Soc. 20(1) (2007), 53–97 (electronic).Google Scholar