Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-09T17:29:43.023Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-monotone periodic orbits of a rotational horseshoe

Published online by Cambridge University Press:  27 November 2017

BRÁULIO A. GARCIA  and
VALENTÍN MENDOZA
BRÁULIO A. GARCIA
Affiliation:
Instituto de Matemática e Computação, Universidade Federal de Itajubá, Av. BPS 1303, Bairro Pinheirinho, CEP 37500-903, Itajubá, MG, Brazil email [email protected], [email protected]
VALENTÍN MENDOZA
Affiliation:
Instituto de Matemática e Computação, Universidade Federal de Itajubá, Av. BPS 1303, Bairro Pinheirinho, CEP 37500-903, Itajubá, MG, Brazil email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we present results for the forcing relation on the set of braid types of periodic orbits of a rotational horseshoe on the annulus. Precisely, we are concerned with a family of periodic orbits, called the Boyland family, and we prove that for each pair 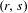$(r,s)$ of rational numbers with $r<s$ in 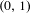$(0,1)$, there exists a non-monotone orbit 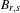$B_{r,s}$ in this family which has pseudo-Anosov type and rotation interval 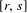$[r,s]$. Furthermore, the forcing relation among these orbits is given by the inclusion order on their rotation sets. It is also proved that the Markov partition associated to each Boyland orbit comes from a pruning map which projects to a bimodal circle map. This family also contains the Holmes orbits 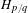$H_{p/q}$, which are the largest for the forcing order among all the 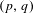$(p,q)$-orbits of the rotational horseshoe.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 7 , July 2019 , pp. 1870 - 1903
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Addas-Zanata, S.. Area-preserving diffeomorphisms of the torus whose rotation sets have non-empty interior. Ergod. Th. & Dynam. Sys. 35 (2015), 1–33.Google Scholar
Aronson, D. G., Chory, M. A., Hall, G. R. and McGeehee, R. P.. Bifurcations from an invariant circle for two-parameter families of maps of the plane: a computer-assisted study. Comm. Math. Phys. 83 (1982), 303–354.Google Scholar
Bernhardt, C.. Rotation intervals of a class of endomorphisms of the circle. Proc. Lond. Math. Soc. (3) 45 (1982), 258–280.Google Scholar
Boyland, P.. An analog of Sharkovski’s theorem for twist maps. Contemp. Math. 81 (1988), 119–133.Google Scholar
Boyland, P.. Rotation sets and monotone periodic orbits for annulus homeomorphisms. Comment. Math. Helv. 67 (1992), 203–213.Google Scholar
Boyland, P.. Topological methods in surface dynamics. Topology Appl. 58 (1994), 223–298.Google Scholar
Bullett, S. and Sentenac, P.. Ordered orbits of the shift, square roots, and the devil’s staircase. Math. Proc. Cambridge Philos. Soc. 115(3) (1994), 451–481.Google Scholar
de Carvalho, A.. Pruning fronts and the formation of horseshoes. Ergod. Th. & Dynam. Sys. 19(4) (1999), 851–894.Google Scholar
de Carvalho, A. and Mendoza, V.. Differentiable pruning and the hyperbolic pruning front conjecture. Preprint, 2014.Google Scholar
Fathi, A., Laudenbach, F. and Poénaru, V.. Travaux de Thurston sur les surfaces. Asterisque 66–67 (1979), article 30.Google Scholar
Franks, J.. Recurrence and fixed points of surface homemomorphisms. Ergod. Th. & Dynam. Sys. 8 (1988), 99–107.Google Scholar
Gambaudo, J. M., Lanford, O. III and Tresser, C.. Dynamique symbolique des rotations. C. R. Acad. Sci. 299 (1984), 823–826.Google Scholar
Goldberg, L. and Tresser, C.. Rotation orbits and the Farey tree. Ergod. Th. & Dynam. Sys. 16 (1996), 1011–1029.Google Scholar
Guckenheimer, J. and Holmes, P.. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York, 1983.Google Scholar
Hall, T.. The creation of horseshoes. Nonlinearity 7 (1994), 861–924.Google Scholar
Handel, M.. Global shadowing of pseudo-Anosov homeomorphisms. Ergod. Th. & Dynam. Sys. 5 (1985), 373–377.Google Scholar
Handel, M.. The rotation set of a homeomorphism of the annulus is closed. Comm. Math. Phys. 127 (1990), 339–349.Google Scholar
Hare, K. and Sidorov, N.. On cycles for the doubling map which are disjoint from an interval. Monatsh. Math. 175 (2014), 347–365.Google Scholar
Hockett, K. and Holmes, P.. Josephson’s junction, annulus maps, Birkhoff attractors, horseshoes and rotation sets. Ergod. Th. & Dynam. Sys. 6 (1986), 205–239.Google Scholar
Holmes, P.. Knotted periodic orbits in suspensions of annulus maps. Proc. R. Soc. Lond. A 411 (1987), 351–378.Google Scholar
Holmes, P.. Knots and orbit genealogies in nonlinear oscillators. New Direction in Dynamical Systems. Eds. Bedford, T. and Swift, J.. Cambridge University Press, Cambridge, 1988.Google Scholar
Holte, S. E. and Roe, R.. Inverse limits associated with the forced van der Pol equation. J. Dynam. Differential Equations 6(4) (1994), 601–612.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.Google Scholar
Levi, M.. Qualitative analysis of the periodically forced relaxation oscillations. Mem. Amer. Math. Soc. 214 (1981), 1–147.Google Scholar
Llibre, J. and Mackay, R. S.. Rotation vectors and entropy for homeomorphisms of the torus isotopic to the identity. Ergod. Th. & Dynam. Sys. 11 (1991), 115–128.Google Scholar
Lothaire, M.. Algebraic Combinatorics on Words (Encyclopedia of Mathematics and its Applications, 90) . Cambridge University Press, Cambridge, 2002.Google Scholar
Mendoza, V.. Dynamics forced by homoclinic orbits. Preprint, 2014.Google Scholar
Mendoza, V.. Ordering horseshoe periodic orbits: pruning models and forcing. Preprint, 2015.Google Scholar
Morse, M. and Hedlund, G.. Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62(1) (1940), 1–42.Google Scholar
Series, C.. The geometry of Markoff numbers. Math. Intelligencer 7 (1985), 20–29.Google Scholar
Veerman, P.. Symbolic dynamics and rotation numbers. Physica A 134 (1986), 543–576.Google Scholar
Veerman, P.. Symbolic dynamics of order preserving orbits. Physica D 29 (1987), 191–201.Google Scholar
Ziemian, K.. Rotation sets for subshifts of finite type. Fund. Math. 146 (1995), 189–201.Google Scholar