Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T01:48:41.128Z Has data issue: false hasContentIssue false
  • English
  • Français

A new look at the crossed product of aC*-algebra by a semigroup of endomorphisms

Published online by Cambridge University Press:  01 June 2008

RUY EXEL
RUY EXEL*
Affiliation:
Departamento de Matemática, Universidade Federal de Santa Catarina, 88040-900, Florianópolis, Brazil (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

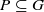Let G be a group and let be a subsemigroup. In order to describe the crossed product of a C*-algebra A by an action of P by unital endomorphisms we find that we must extend the action to the whole group G. This extension fits into a broader notion of interaction groups which consists of an assignment of a positive operator Vg on A for each g in G, obeying a partial group law, and such that (Vg,Vg−1) is an interaction for every g, as defined in a previous paper by the author. We then develop a theory of crossed products by interaction groups and compare it to other endomorphism crossed product constructions.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 3 , June 2008 , pp. 749 - 789
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bratteli, O. and Robinson, D. W.. Operator Algebras and Quantum Statistical Mechanics, 2 (Texts and Monographs in Physics). Springer, Berlin, 1997.CrossRefGoogle Scholar
[2]Brownlowe, N. and Raeburn, I.. Exel’s crossed product and relative Cuntz–Pimsner algebras. Math. Proc. Cambridge Philos. Soc. 141(3) (2006), 497–508 [arXiv:math.OA/0408324].CrossRefGoogle Scholar
[3]Cuntz, J.. Simple C *-algebras generated by isometries. Comm. Math. Phys. 57 (1977), 173–185.CrossRefGoogle Scholar
[4]Cuntz, J.. Automorphisms of certain simple C *-algebras. Quantum Fields—Algebras, Processes (Proc. Sympos., Univ. Bielefeld, Bielefeld, 1978). Springer, Vienna, 1980, pp. 187–196.CrossRefGoogle Scholar
[5]Exel, R.. Amenability for Fell bundles. J. Reine Angew. Math. 492 (1997), 41–73 [arXiv:funct-an/9604009], MR 99a:46131.Google Scholar
[6]Exel, R.. Partial actions of groups and actions of inverse semigroups. Proc. Amer. Math. Soc. 126 (1998), 3481–3494 [arXiv:funct-an/9511003], MR 99b:46102.CrossRefGoogle Scholar
[7]Exel, R.. A new look at the crossed-product of a C *-algebra by an endomorphism. Ergod. Th. & Dynam. Sys. 23 (2003), 1733–1750 [arXiv:math.OA/0012084].CrossRefGoogle Scholar
[8]Exel, R.. Interactions. J. Funct. Anal. 244(1) (2007), 26–62 [arXiv:math.OA/0409267].CrossRefGoogle Scholar
[9]Exel, R. and Renault, J.. Semigroups of local homeomorphisms and interaction groups. Ergod. Th. & Dynam. Sys. 27(6) (2007), 1737–1771 [arXiv:math.OA/0608589].CrossRefGoogle Scholar
[10]Exel, R. and Vershik, A.. C *-algebras of irreversible dynamical systems. Canad. J. Math. 58 (2006), 39–63 [arXiv:math.OA/0203185].CrossRefGoogle Scholar
[11]Fell, J. M. G. and Doran, R. S.. Representations of *-Algebras, Locally Compact Groups, and Banach *-Algebraic Bundles (Pure and Applied Mathematics, 125 and 126). Academic Press, Boston, 1988.Google Scholar
[12]Fowler, N. J.. Discrete product systems of Hilbert bimodules. Pacific J. Math. 204 (2002), 335–375.CrossRefGoogle Scholar
[13]Katsura, T.. A construction of C *-algebras from C *-correspondences. Advances in Quantum Dynamics (South Hadley, MA, 2002) (Contemporary Mathematics). American Mathematical Society, Providence, RI, 2003, pp. 173–182 [arXiv:math.OA/0309059].CrossRefGoogle Scholar
[14]Kirchberg, E. and Wassermann, S.. Operations on continuous bundles of C *-algebras. Math. Ann. 303(4) (1995), 677–697.CrossRefGoogle Scholar
[15]Laca, M. and Raeburn, I.. Semigroup crossed products and Toeplitz algebras of non-abelian groups. J. Funct. Anal. 139 (1996), 415–440.CrossRefGoogle Scholar
[16]Larsen, N. S.. Crossed products by abelian semigroups via transfer operators. Preprint, 2005 [arXiv:math.OA/0502307].Google Scholar
[17]Pimsner, M. V.. A class of C *-algebras generalizing both Cuntz–Krieger algebras and crossed products by . Fields Inst. Commun. 12 (1997), 189–212.Google Scholar
[18]Renault, J.. A Groupoid Approach to C *-algebras (Lecture Notes in Mathematics, 793). Springer, Berlin, 1980.CrossRefGoogle Scholar
[19]Takesaki, M.. Theory of Operator Algebras, I. Springer, Berlin, 1979.CrossRefGoogle Scholar