Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T01:07:09.375Z Has data issue: false hasContentIssue false
  • English
  • Français

Necessary and sufficient conditions for a maximal ergodic theorem along subsequences

Published online by Cambridge University Press:  19 September 2008

Roger L. Jones
Roger L. Jones
Affiliation:
Department of Mathematics, DePaul University, Chicago, IL 60614, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T be an ergodic measure preserving point transformation from a probability space X onto itself. Assume that 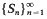is an increasing sequence of subsets of the positive integers. Conditions are given which are sufficient for the ergodic maximal function associated with these subsets to be weak type (p, p). These conditions are shown to be both necessary and sufficient for a larger two-sided maximal function. The conditions are in the form of covering lemmas for the integers.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 7 , Issue 2 , June 1987 , pp. 203 - 210
Copyright
Copyright © Cambridge University Press 1987

References

REFERENCES

[1]Bellow, A.. Manuscript in preparation.Google Scholar
[2]Bellow, A. & Losert, V.. On sequences of density zero in ergodic theory. Contemporary Mathematics 28 (1984), 49–60.Google Scholar
[3]Corboda, A. & Fefferman, R.. A geometric proof of the strong maximal theorem. Annals of Math. 102 (1975), 95–100.Google Scholar
[4]Soria, F.. Personal communication.Google Scholar