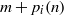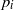Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
SCHNURR, MIKE
2019.
Generic properties of extensions.
Ergodic Theory and Dynamical Systems,
Vol. 39,
Issue. 11,
p.
3144.
Farhangi, Sohail
2024.
Van der Corput’s difference theorem for amenable groups and the left regular representation.
Indagationes Mathematicae,