Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T02:54:29.522Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple recurrence and convergence for certain averages along shifted primes

Published online by Cambridge University Press:  04 June 2014

WENBO SUN Open the ORCID record for WENBO SUN [Opens in a new window]
WENBO SUN*
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Road, Evanston, IL 60208-2730, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that any subset 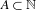$A\subset \mathbb{N}$ with positive upper Banach density contains the pattern 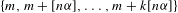$\{m,m+[n{\it\alpha}],\dots ,m+k[n{\it\alpha}]\}$, for some 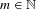$m\in \mathbb{N}$ and 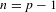$n=p-1$ for some prime 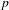$p$, where 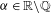${\it\alpha}\in \mathbb{R}\setminus \mathbb{Q}$. Making use of the Furstenberg correspondence principle, we do this by proving an associated recurrence result in ergodic theory along the shifted primes. We also prove the convergence result for the associated averages along primes and indicate other applications of these methods.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 5 , August 2015 , pp. 1592 - 1609
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergelson, V.. Weakly mixing PET. Ergod. Th. & Dynam. Sys. 7 (1987), 337–349.CrossRefGoogle Scholar
Bergelson, V. and Håland, I. J.. Sets of recurrence and generalized polynomials. Convergence in Ergodic Theory and Probability (Columbus, OH, 1993) (Ohio State University Mathematics Research Institute Publications, 5). de Gruyter, Berlin, 1996, pp. 91–110.CrossRefGoogle Scholar
Bergelson, V., Host, B. and Kra, B.. Multiple recurrence and nilsequences. Invent. Math. 160(2) (2005), 261–303 (with an appendix by I. Rusza).CrossRefGoogle Scholar
Bergelson, V., Host, B., McCutcheon, R. and Parreau, F.. Aspects of uniformity in recurrence. Colloq. Math. 84/85(2) (2000), 549–576.CrossRefGoogle Scholar
Bergelson, V., Leibman, A. and Ziegler, T.. The shifted primes and the multidimensional Szemerédi and polynomial van der Waerden theorems. C. R. Math. Acad. Sci. Paris 349(3–4) (2011), 123–125.CrossRefGoogle Scholar
Frantzikinakis, N.. Equidistribution of sparse sequences on nilmanifolds. J. Anal. Math. 109 (2009), 1–43.CrossRefGoogle Scholar
Frantzikinakis, N.. Multiple recurrence and convergence for Hardy sequences of polynomial growth. J. Anal. Math. 112 (2010), 79–135.CrossRefGoogle Scholar
Frantzikinakis, N., Host, B. and Kra, B.. Multiple recurrence and convergence for sequences related to the prime numbers. J. Reine Angew. Math. 611 (2007), 131–144.Google Scholar
Frantzikinakis, N., Host, B. and Kra, B.. The polynomial multidimensional Szemerédi theorem along shifted primes. Israel J. Math. to appear. Preprint, arXiv:1009.1484.Google Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 71 (1977), 204–256.CrossRefGoogle Scholar
Furstenberg, H. and Weiss, B.. A mean ergodic theorem for (1∕N)∑n=1Nf (T nx)g (T n 2x). Convergence in Ergodic Theory and Probability. Walter de Gruyter, Berlin, 1996, pp. 193–227.CrossRefGoogle Scholar
Gowers, W.. A new proof of Szemerédi theorem. Geom. Funct. Anal. 11 (2001), 465–588.CrossRefGoogle Scholar
Green, B. and Tao, T.. Linear equations in primes. Ann. of Math. (2) 171(3) (2010), 1753–1850.CrossRefGoogle Scholar
Green, B. and Tao, T.. The Möbius function is strongly orthogonal to nilsequences. Ann. of Math. (2) 175(2) (2012), 541–566.CrossRefGoogle Scholar
Green, B. and Tao, T.. The primes contain arbitrarily long arithmetic progressions. Ann. of Math. (2) 167 (2008), 481–547.CrossRefGoogle Scholar
Green, B., Tao, T. and Ziegler, T.. An inverse theorem for the Gowers U s+1-norm. Ann. of Math. (2) 176(2) (2012), 1231–1372.CrossRefGoogle Scholar
Host, B. and Kra, B.. Convergence of polynomial ergodic averages. Israel J. Math. 149 (2005), 1–19.CrossRefGoogle Scholar
Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161(1) (2005), 397–488.CrossRefGoogle Scholar
Host, B. and Kra, B.. Uniformity seminorms on l ∞ and applications. J. Anal. Math. 108 (2009), 219–276.CrossRefGoogle Scholar
Kuipers, L. and Niederreiter, H.. Uniform distribution of sequences. Pure and Applied Mathematics. Wiley-Interscience, New York, 1974.Google Scholar
Leibman, A.. Convergence of multiple ergodic averages along polynomials of several variables. Israel J. Math. 146 (2005), 303–316.CrossRefGoogle Scholar
Leibman, A.. Pointwise convergence of ergodic averages for polynomial sequences of translations on a nilmanifold. Ergod. Th. & Dynam. Sys. 25(1) (2005), 201–213.CrossRefGoogle Scholar
Sarközy, A.. On difference sets of sequences of integers, III. Acta Math. Hungar. 31 (1978), 355–386.CrossRefGoogle Scholar
Wooley, T. D. and Ziegler, T. D.. Multiple recurrence and convergence along the primes. Amer. J. Math. 134(6) (2012), 1705–1732.CrossRefGoogle Scholar
Ziegler, T.. Universal characteristic factors and Furstenberg averages. J. Amer. Math. Soc. 20 (2007), 53–97.CrossRefGoogle Scholar