No CrossRef data available.
Published online by Cambridge University Press: 03 February 2023
We consider the family 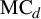 $\mathrm {MC}_d$ of monic centered polynomials of one complex variable with degree
$\mathrm {MC}_d$ of monic centered polynomials of one complex variable with degree 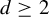 $d \geq 2$, and study the map
$d \geq 2$, and study the map 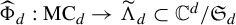 $\widehat {\Phi }_d:\mathrm {MC}_d\to \widetilde {\Lambda }_d \subset \mathbb {C}^d / \mathfrak {S}_d$ which maps each
$\widehat {\Phi }_d:\mathrm {MC}_d\to \widetilde {\Lambda }_d \subset \mathbb {C}^d / \mathfrak {S}_d$ which maps each 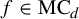 $f \in \mathrm {MC}_d$ to its unordered collection of fixed-point multipliers. We give an explicit formula for counting the number of elements of each fiber
$f \in \mathrm {MC}_d$ to its unordered collection of fixed-point multipliers. We give an explicit formula for counting the number of elements of each fiber 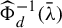 $\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} })$ for every
$\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} })$ for every 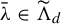 $\bar {\unicode{x3bb} } \in \widetilde {\Lambda }_d$ except when the fiber
$\bar {\unicode{x3bb} } \in \widetilde {\Lambda }_d$ except when the fiber 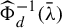 $\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} })$ contains polynomials having multiple fixed points. This formula is not a recursive one, and is a drastic improvement of our previous result [T. Sugiyama. The moduli space of polynomial maps and their fixed-point multipliers. Adv. Math. 322 (2017), 132–185] which gave a rather long algorithm with some induction processes.
$\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} })$ contains polynomials having multiple fixed points. This formula is not a recursive one, and is a drastic improvement of our previous result [T. Sugiyama. The moduli space of polynomial maps and their fixed-point multipliers. Adv. Math. 322 (2017), 132–185] which gave a rather long algorithm with some induction processes.