Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T01:07:58.010Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing properties of (α,β)-expansions

Published online by Cambridge University Press:  01 August 2009

KARMA DAJANI ,
YUSUF HARTONO  and
COR KRAAIKAMP
KARMA DAJANI
Affiliation:
Department of Mathematics, Utrecht University, Postbus 80.000, 3508 TA Utrecht, The Netherlands (email: [email protected])
YUSUF HARTONO
Affiliation:
Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sriwijaya, Jalan Raya Palembang Prabumulih Km 32, Indralaya 30662, Indonesia (email: [email protected])
COR KRAAIKAMP
Affiliation:
Delft University of Technology and Thomas Stieltjes Institute for Mathematics, EWI (DIAM), Mekelweg 4, 2628 CD Delft, The Netherlands (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 0<α<1 and β>1. We show that every x∈[0,1] has an expansion of the form 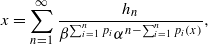where hi=hi(x)∈{0,α/β}, and pi=pi(x)∈{0,1}. We study the dynamical system underlying this expansion and give the density of the invariant measure that is equivalent to the Lebesgue measure. We prove that the system is weakly Bernoulli, and we give a version of the natural extension. For special values of α, we give the relationship of this expansion with the greedy β-expansion.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 29 , Issue 4 , August 2009 , pp. 1119 - 1140
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Barrionuevo, J., Burton, R. M., Dajani, K. and Kraaikamp, C.. Ergodic properties of generalized Lüroth series. Acta Arith. 74(4) (1996), 311–327.CrossRefGoogle Scholar
[2]Boudourides, M. A. and Fotiades, N. A.. Piecewise linear interval maps both expanding and contracting. Dyn. Stab. Syst. 15(4) (2000), 343–351.CrossRefGoogle Scholar
[3]Bosma, W., Jager, H. and Wiedijk, F.. Some metrical observations on the approximation by continued fractions. Nederl. Akad. Wetensch. Indag. Math. 45(3) (1983), 281–299.CrossRefGoogle Scholar
[4]Coelho, Z., Lopes, A. and da Rocha, L. F.. Absolutely continuous invariant measures for a class of affine interval exchange maps. Proc. Amer. Math. Soc. 123(11) (1995), 3533–3542.CrossRefGoogle Scholar
[5]Dajani, K. and Kraaikamp, C.. Ergodic Theory of Numbers (Carus Mathematical Monographs, 29). Mathematical Association of America, Washington, DC, 2002.CrossRefGoogle Scholar
[6]Dajani, K., Kraaikamp, C. and Solomyak, B.. The natural extension of the β-transformation. Acta Math. Hungar. 73(1-2) (1996), 97–109.CrossRefGoogle Scholar
[7]Eslami, P. and Gora, P.. Eventually expanding maps. Preprint, 2008, arXiv.org/pdf/0807.4715.Google Scholar
[8]Flatto, L. and Lagarias, J. C.. The lap-counting function for linear mod one transformations. III. The period of a Markov chain. Ergod. Th. & Dynam. Sys. 17(2) (1997), 369–403.CrossRefGoogle Scholar
[9]Gel’fond, A. O.. A common property of number systems. Izv. Akad. Nauk SSSR. Ser. Mat. 23 (1959), 809–814.Google Scholar
[10]Góra, P.. Invariant densities for generalized β-maps. Ergod. Th. & Dynam. Sys. 27(05) (2007), 1583–1598.CrossRefGoogle Scholar
[11]Islam, S.. Absolutely continuous invariant measures of linear interval maps. Int. J. Pure Appl. Math. 27(4) (2006), 4449–4464.Google Scholar
[12]Iosifescu, M. and Kraaikamp, C.. Metrical Theory of Continued Fractions (Mathematics and Its Applications, 547). Kluwer, Dordrecht, 2002.CrossRefGoogle Scholar
[13]Kopf, C.. Invariant measures for piecewise linear transformations of the interval, part II. Appl. Math. Comput. 39(2) (1990), 123–144.Google Scholar
[14]Palmer, M. R.. On the classification of measure preserving transformations of Lebesgue spaces. PhD. Thesis, University of Warwick, 1979.Google Scholar
[15]Parry, W.. On the β-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.CrossRefGoogle Scholar
[16]Rényi, A.. On algorithms for the generation of real numbers. Magyar Tud. Akad. Mat. Fiz. Oszt. Közl. 7 (1957), 265–293.Google Scholar
[17]Rényi, A.. Representations for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hungar. 8 (1957), 477–493.CrossRefGoogle Scholar
[18]Rohlin, V. A.. Exact endomorphisms of a Lebesgue space. Izv. Akad. Nauk SSSR Ser. Mat. 25 (1961), 499–530; Engl. Trans. Amer. Math. Soc. Transl. 39(2) (1964), 1–36.Google Scholar
[19]Rychlik, M.. Bounded variation and invariant measures. Studia Math. 76 (1983), 69–80.CrossRefGoogle Scholar
[20]Saleski, A.. On induced transformations of Bernoulli shifts. Math. Systems Theory 7 (1973), 83–96.CrossRefGoogle Scholar
[21]Wilkinson, K. M.. Ergodic properties of certain linear mod one transformations. Adv. Math. 14 (1974), 64–72.CrossRefGoogle Scholar
[22]Wilkinson, K. M.. Ergodic properties of a class of piecewise linear transformations. Z. Wahrs. Verw. Gebiete 31 (1974/75), 303–328.CrossRefGoogle Scholar