Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T01:58:16.753Z Has data issue: false hasContentIssue false
  • English
  • Français

A mixing completely scrambled system exists

Published online by Cambridge University Press:  04 May 2017

JAN P. BOROŃSKI ,
JIŘÍ KUPKA  and
PIOTR OPROCHA
JAN P. BOROŃSKI
Affiliation:
AGH University of Science and Technology, Faculty of Applied Mathematics, al. Mickiewicza 30, 30-059 Kraków, Poland email [email protected], [email protected] National Supercomputing Centre IT4Innovations, Division of the University of Ostrava, Institute for Research and Applications of Fuzzy Modeling, 30. dubna 22, 70103 Ostrava, Czech Republic email [email protected]
JIŘÍ KUPKA
Affiliation:
National Supercomputing Centre IT4Innovations, Division of the University of Ostrava, Institute for Research and Applications of Fuzzy Modeling, 30. dubna 22, 70103 Ostrava, Czech Republic email [email protected]
PIOTR OPROCHA
Affiliation:
AGH University of Science and Technology, Faculty of Applied Mathematics, al. Mickiewicza 30, 30-059 Kraków, Poland email [email protected], [email protected] National Supercomputing Centre IT4Innovations, Division of the University of Ostrava, Institute for Research and Applications of Fuzzy Modeling, 30. dubna 22, 70103 Ostrava, Czech Republic email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that there exists a topologically mixing homeomorphism which is completely scrambled. We also prove that, for any integer 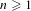$n\geq 1$, there is a continuum of topological dimension $n$ supporting a transitive completely scrambled homeomorphism and an $n$-dimensional compactum supporting a weakly mixing completely scrambled homeomorphism. This solves a 15-year-old open problem.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 1 , January 2019 , pp. 62 - 73
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E., Auslander, J. and Berg, K.. When is a transitive map chaotic? Convergence in Ergodic Theory and Probability (Columbus, OH, 1993). de Gruyter, Berlin, 1996, pp. 25–40.Google Scholar
Akin, E. and Kolyada, S.. Li–Yorke sensitivity. Nonlinearity 16 (2003), 1421–1433.Google Scholar
Akin, E., Glasner, E. and Weiss, B.. Generically there is but one self homeomorphism of the Cantor set. Trans. Amer. Math. Soc. 360 (2008), 3613–3630.Google Scholar
Blanchard, F., Huang, W. and Snoha, L.. Topological size of scrambled sets. Colloq. Math. 110 (2008), 293–361.Google Scholar
Boroński, J., Clark, A. and Oprocha, P.. New exotic minimal sets from pseudosuspensions of Cantor systems. Preprint, 2016, arXiv:1609.09121 [math.DS].Google Scholar
Bruckner, A. M. and Hu, T.. On scrambled sets for chaotic functions. Trans. Amer. Math. Soc. 301 (1987), 289–297.Google Scholar
Fayad, B.. Topologically mixing and minimal but not ergodic, analytic transformation on T5 . Bol. Soc. Brasil. Mat. (N.S.) 31 (2000), 277–285.Google Scholar
Foryś, M., Huang, W., Li, J. and Oprocha, P.. Invariant scrambled sets, uniform rigidity and weak mixing. Israel J. Math. 211 (2016), 447–472.Google Scholar
Gedeon, T.. There are no chaotic mappings with residual scrambled sets. Bull. Aust. Math. Soc. 36 (1987), 411–416.Google Scholar
Glasner, S. and Maon, D.. Rigidity in topological dynamics. Ergod. Th. & Dynam. Sys. 9 (1989), 309–320.Google Scholar
Glasner, S. and Weiss, B.. On the construction of minimal skew products. Israel J. Math. 34 (1979), 321–336.Google Scholar
Handel, M.. A pathological area preserving C ∞ diffeomorphism of the plane. Proc. Amer. Math. Soc. 86 (1982), 163–168.Google Scholar
Huang, W. and Ye, X.. Homeomorphisms with the whole compacta being scrambled sets. Ergod. Th. & Dynam. Sys. 21 (2001), 77–91.Google Scholar
Li, T. Y. and Yorke, J.. Period three implies chaos. Amer. Math. Monthly 82 (1975), 985–992.Google Scholar
Mai, J.. Scrambled sets of continuous maps of 1-dimensional polyhedra. Trans. Amer. Math. Soc. 351 (1999), 353–362.Google Scholar
Misiurewicz, M.. Chaos almost everywhere. Iteration Theory and its Functional Equations (Lochau, 1984) (Lecture Notes in Mathematics, 1163) . Springer, Berlin, 1985, pp. 125–130.Google Scholar
Shimomura, T.. Special homeomorphisms and approximation for Cantor systems. Topol. Appl. 161 (2014), 178–195.Google Scholar
Shimomura, T.. The construction of a completely scrambled system by graph covers. Proc. Amer. Math. Soc. 144 (2016), 2109–2120.Google Scholar