Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T15:33:33.633Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing actions of the Heisenberg group

Published online by Cambridge University Press:  21 January 2013

ALEXANDRE I. DANILENKO
ALEXANDRE I. DANILENKO*
Affiliation:
Institute for Low Temperature Physics & Engineering of National Academy of Sciences of Ukraine, 47 Lenin Avenue, Kharkov, 61164, Ukraine email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Mixing (of all orders) rank-one actions 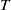$T$ of the Heisenberg group 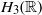${H}_{3} ( \mathbb{R} )$ are constructed. The restriction of 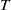$T$ to the center of 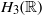${H}_{3} ( \mathbb{R} )$ is simple and commutes only with 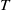$T$. Mixing Poisson and mixing Gaussian actions of 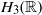${H}_{3} ( \mathbb{R} )$ are also constructed. A rigid weakly mixing rank-one action 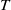$T$ is constructed such that the restriction of 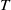$T$ to the center of 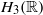${H}_{3} ( \mathbb{R} )$ is not isomorphic to its inverse.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 4 , August 2014 , pp. 1142 - 1167
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, T. M.. Smorodinsky’s conjecture on rank-one mixing. Proc. Amer. Math. Soc. 126 (1998), 739–744.Google Scholar
Adams, T. and Silva, C. E.. ${ \mathbb{Z} }^{d} $-staircase actions. Ergod. Th. & Dynam. Sys. 19 (1999), 837–850.Google Scholar
Cornfeld, I., Fomin, S. and Sinai, Ya. G.. Ergodic Theory. Springer, New York, 1982.Google Scholar
Creutz, D. and Silva, C. E.. Mixing on a class of rank-one transformations. Ergod. Th. & Dynam. Sys. 24 (2004), 407–440.Google Scholar
Danilenko, A. I.. Funny rank-one weak mixing for nonsingular Abelian actions. Israel J. Math. 121 (2001), 29–54.Google Scholar
Danilenko, A. I.. Mixing rank-one actions for infinite sums of finite groups. Israel J. Math. 156 (2006), 341–358.Google Scholar
Danilenko, A. I.. $(C, F)$-actions in ergodic theory. Progr. Math. 265 (2008), 325–351.Google Scholar
Danilenko, A. I.. Uncountable collection of mixing rank-one actions for locally normal groups. Semin. et Congr. de la SMF 20 (2011), 253–266.Google Scholar
Danilenko, A. I. and Dooley, A. H.. Simple ${ \mathbb{Z} }^{2} $-actions twisted by aperiodic automorphisms. Israel J. Math. 175 (2010), 285–299.Google Scholar
Danilenko, A. I. and Ryzhikov, V. V.. On self-similarities of ergodic flows. Proc. Lond. Math. Soc. 104 (2012), 431–454.Google Scholar
Danilenko, A. I. and Silva, C. E.. Mixing rank-one actions of locally compact Abelian groups. Ann. Inst. Henri Poincaré Probab. Stat. 43 (2007), 375–398.Google Scholar
Danilenko, A. I. and Silva, C. E.. Ergodic Theory: Nonsingular Transformations (Encyclopedia of Complexity and Systems Science). Ed. Meyers, R. A.. Springer, Berlin, 2009, pp. 3055–3083.Google Scholar
del Junco, A.. A simple map with no prime factors. Israel J. Math. 104 (1998), 301–320.Google Scholar
del Junco, A. and Rudolph, D.. On ergodic actions whose self-joinings are graphs. Ergod. Th. & Dynam. Sys. 7 (1987), 531–557.Google Scholar
de la Rue, T.. Joinings in Ergodic Theory (Encyclopedia of Complexity and Systems Science). Ed. Meyers, R. A.. Springer, Berlin, 2009, pp. 5037–5051.Google Scholar
Fayad, B.. Rank one and mixing differentiable flows. Invent. Math. 160 (2005), 305–340.Google Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets and diophantine approximation. Math. Syst. Th. 1 (1967), 1–49.Google Scholar
Glasner, E.. Ergodic Theory via Joinings. American Mathematical Society, Providence, RI, 2003.Google Scholar
Kirillov, A. A.. Lectures on the Orbit Method. American Mathematical Society, Providence, RI, 2004.Google Scholar
Leonov, V. P.. The use of the characteristic functional and semi-invariants in the ergodic theory of stationary processes. Dokl. Akad. Nauk SSSR 133 (1960), 523–526 (in Russian).Google Scholar
Mackey, G. W.. Borel structure in groups and their duals. Trans. Amer. Math. Soc. 85 (1957), 134–169.Google Scholar
Ornstein, D. S.. On the root problem in ergodic theory. Proc. Sixth Berkley Symp. Math. Stat. Prob. (University of California, Berkeley, CA, 1970/1971). Vol. II. University of California Press, Berkeley, CA, 1972, pp. 347–356.Google Scholar
Ornstein, D. S. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48 (1987), 1–141.Google Scholar
Prikhodko, A.. Stochastic constructions of flows of rank one. Mat. Sb. 192 (2001), 61–92.Google Scholar
Roy, E.. Ergodic properties of Poisson ID processes. Ann. Probab. 35 (2007), 551–576.Google Scholar
Rudolph, D.. An example of a measure-preserving map with minimal self-joinings, and applications. J. Anal. Math. 35 (1979), 97–122.Google Scholar
Ryzhikov, V. V.. Skew products and multiple mixing of dynamical systems. Russian Math. Surveys 49 (1994), 170–171.Google Scholar
Ryzhikov, V. V.. Stochastic intertwinings and multiple mixing of dynamical systems. J. Dyn. Control Syst. 2 (1996), 1–19.Google Scholar
Ryzhikov, V. V.. On the asymmetry of cascades. Proc. Steklov Inst. Math. 216 (1997), 147–150.Google Scholar
Ryzhikov, V. V.. Around simple dynamical systems. Induced joinings and multiple mixing. J. Dyn. Control Syst. 3 (1997), 111–127.Google Scholar
Ryzhikov, V. V.. On mixing rank one infinite transformations. Preprint, 2011, arXiv: 1106.4655.Google Scholar
Thouvenot, J.-P.. Some properties and applications of joinings in ergodic theory. Ergodic Theory and its Connections with Harmonic Analysis (Alexandria, 1993) (London Mathematical Society Lecture Note Series, 205), Cambridge University Press, Cambridge, 1995, pp. 207–235.Google Scholar
Weiss, B.. Monotilable amenable groups. Topology, Ergodic Theory, Real Algebraic Geometry (American Mathematical Society Translations Series 2, 202), American Mathematical Society, Providence, RI, 2001, pp. 257–262.Google Scholar