Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:26:22.299Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal interval exchange transformations with flips

Published online by Cambridge University Press:  03 April 2017

ANTONIO LINERO BAS  and
GABRIEL SOLER LÓPEZ Open the ORCID record for GABRIEL SOLER LÓPEZ [Opens in a new window]
ANTONIO LINERO BAS
Affiliation:
Departamento de Matemáticas, Universidad de Murcia (Campus de Espinardo), 30100-Espinardo-Murcia, Spain email [email protected]
GABRIEL SOLER LÓPEZ
Affiliation:
Departamento de Matemática Aplicada y Estadística, Paseo Alfonso XIII, 52, 30203-Cartagena, Spain email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

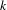We consider interval exchange transformations of $n$ intervals with $k$ flips, or 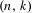$(n,k)$-IETs for short, for positive integers 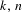$k,n$ with 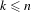$k\leq n$. Our main result establishes the existence of minimal uniquely ergodic $(n,k)$-IETs when 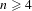$n\geq 4$; moreover, these IETs are self-induced for 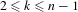$2\leq k\leq n-1$. This result extends the work on transitivity in Gutierrez et al [Transitive circle exchange transformations with flips. Discrete Contin. Dyn. Syst. 26(1) (2010), 251–263]. In order to achieve our objective we make a direct construction; in particular, we use the Rauzy induction to build a periodic Rauzy graph whose associated matrix has a positive power. Then we use a result in the Perron–Frobenius theory [Pullman, A geometric approach to the theory of non-negative matrices. Linear Algebra Appl. 4 (1971) 297–312] which allows us to ensure the existence of these minimal self-induced and uniquely ergodic 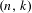$(n,k)$-IETs, 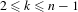$2\leq k\leq n-1$. We then find other permutations in the same Rauzy class generating minimal uniquely ergodic 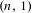$(n,1)$- and 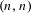$(n,n)$-IETs.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 8 , December 2018 , pp. 3101 - 3144
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angosto Hernández, C. and Soler López, G.. Minimality and the Rauzy–Veech algorithm for interval exchange transformations with flips. Dyn. Syst. 28(4) (2013), 539–550.Google Scholar
Arnoux, P.. Échanges d’intervalles et flots sur les surfaces. Monogr. Enseign. Math. 29 (1981), 5–38.Google Scholar
Avila, A. and Viana, M.. Dynamics in the moduli space of Abelian differentials. Port. Math. 62(4) (2005), 531–547.Google Scholar
Avila, A. and Viana, M.. Simplicity of Lyapunov spectra: proof of the Zorich–Kontsevich conjecture. Acta Math. 198(1) (2007), 1–56.Google Scholar
Benière, J.-C.. Feuilletage minimaux sur les surfaces non compactes. Thèse d’État, Université de Lyon, 1998.Google Scholar
Cornfeld, I. P., Fomin, S. V. and Sinaĭ, Ya. G.. Ergodic Theory (Grundlehren der Mathematischen Wissenschaften, 245) . Springer, New York, 1982.Google Scholar
Danthony, C. and Nogueira, A.. Involutions linéaires et feuilletages mesurés. C. R. Acad. Sci. Paris Sér. I Math. 307(8) (1988), 409–412.Google Scholar
Danthony, C. and Nogueira, A.. Measured foliations on nonorientable surfaces. Ann. Sci. Éc. Norm. (4) 23(3) (1990), 469–494.Google Scholar
Espín Buendía, J. G., Peralta-Salas, D. and Soler López, G.. Existence of minimal flows on nonorientable surfaces. Preprint, 2016, arXiv:1608.08788v1.Google Scholar
Gutierrez, C.. Smooth nonorientable nontrivial recurrence on two-manifolds. J. Differential Equations 29 (1978), 388–395.Google Scholar
Gutierrez, C.. Smoothing continuous flows on two-manifolds and recurrences. Ergod. Th. & Dynam. Sys. 6 (1986), 17–44.Google Scholar
Gutierrez, C., Lloyd, S., Medvedev, V., Pires, B. and Zhuzhoma, E.. Transitive circle exchange transformations with flips. Discrete Contin. Dyn. Syst. 26(1) (2010), 251–263.Google Scholar
Gutierrez, C., Lloyd, S. and Pires, B.. Affine interval exchange transformations with flips and wandering intervals. Proc. Amer. Math. Soc. 137(4) (2009), 1439–1445.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54) . Cambridge University Press, Cambridge, 1995, with a supplement by Anatole Katok and Leonardo Mendoza.Google Scholar
Keane, M.. Interval exchange transformations. Math. Z. 141 (1975), 25–31.Google Scholar
Keane, M.. Non-ergodic interval exchange transformations. Israel J. Math. 26 (1977), 188–196.Google Scholar
Keynes, H. and Newton, D.. A ‘minimal’, non-uniquely ergodic interval exchange transformation. Math. Z. 148 (1976), 101–105.Google Scholar
Kontsevich, M. and Zorich, A.. Connected components of the moduli spaces of Abelian differentials with prescribed singularities. Invent. Math. 153 (2003), 631–678.Google Scholar
Levitt, G.. Pantalons et feuilletages des surfaces. Topology 21(1) (1982), 9–33.Google Scholar
Mañé, R.. Ergodic Theory and Differentiable Dynamics (Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 8) . Springer, Berlin, 1987, translated from the Portuguese by Silvio Levy.Google Scholar
Masur, H.. Interval exchange transformations and measured foliations. Ann. of Math. (2) 115 (1982), 169–200.Google Scholar
Masur, H. and Tabachnikov, S.. Rational billiards and flat structures. Handbook of Dynamical Systems, Vol. 1A. North-Holland, Amsterdam, 2002, pp. 1015–1089.Google Scholar
Nogueira, A.. Nonorientable recurrence of flows and interval exchange transformations. J. Differential Equations 70 (1987), 153–166.Google Scholar
Nogueira, A.. Almost all interval exchange transformatios with flips are nonergodic. Ergod. Th. & Dynam. Sys. 9 (1989), 515–525.Google Scholar
Nogueira, A., Pires, B. and Troubetzkoy, S.. Orbit structure of interval exchange transformations with flip. Nonlinearity 26(2) (2013), 525–537.Google Scholar
Pullman, N. J.. A geometric approach to the theory of nonnegative matrices. Linear Algebra Appl. 4 (1971), 297–312.Google Scholar
Rauzy, G.. Échanges d’intervalles et transformations induites. Acta Arith. 34(4) (1979), 315–328.Google Scholar
Sataev, E. A.. The number of invariant measures for flows on orientable surfaces. Izv. Akad. Nauk SSSR Ser. Mat. 39(4) (1975), 860–878 (in Russian) (English translation in Math. USSR Izvestija 9(4) (1975), 813–830).Google Scholar
Soler López, G.. Transitive and minimal flows and interval exchange transformations. Advances in Discrete Dynamics. Nova Science Publishers, New York, 2013, Ch. 5.Google Scholar
Veech, W. A.. Interval exchange transformations. J. Anal. Math. 33 (1978), 222–272.Google Scholar
Veech, W. A.. Gauss measures for transformations on the space of interval exchange maps. Ann. of Math. (2) 115 (1982), 201–242.Google Scholar
Viana, M.. Ergodic theory of interval exchange maps. Rev. Mat. Complut. 19(1) (2006), 7–100.Google Scholar
Yoccoz, J.-C.. Continued fraction algorithms for interval exchange maps: an introduction. Frontiers in Number Theory, Physics, and Geometry. I. Springer, Berlin, 2006, pp. 401–435.Google Scholar