Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T12:46:03.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal entropy and Mostow's rigidity theorems

Published online by Cambridge University Press:  19 September 2008

Gérard Besson ,
Gilles Courtois  and
Sylvestre Gallot
Gérard Besson
Affiliation:
Institut Fourier-C.N.R.S., U.R.A. 188, B.P. 74, 38402 Saint Martin d'Héres Cedex, France
Gilles Courtois
Affiliation:
École Polytechnique-C.N.R.S., U.R.A. 169, Centre de Mathématiques, 91128 Palaiseau Cedex, France
Sylvestre Gallot
Affiliation:
École Normale Supérieure de Lyon, U.M.R. 128, 46, Allée d'Italie, 69364 Lyon Cedex 07, France
Get access Rights & Permissions [Opens in a new window]

Extract

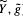Let (Y, g) be a compact connected n-dimensional Riemannian manifold and let () be its universal cover endowed with the pulled-back metric. If y ∈ 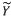, we define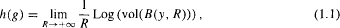

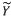where B(y, R) denotes the ball of radius R around y in . It is a well known fact that this limit exists and does not depend on y ([Man]). The invariant h(g) is called the volume entropy of the metric g but, for the sake of simplicity, we shall use the term entropy. The idea of recognizing special metrics in terms of this invariant looks at first glance very optimistic. First the entropy, which behaves like the inverse of a distance, is sensitive to changes of scale which makes it a bad invariant: however, this is a minor drawback that can be circumvented by looking at the behaviour of the entropy functional on the space of metrics with fixed volume (equal to one for example). Nevertheless, it seems very unlikely that two numbers, the entropy and the volume, might characterize any metric. The very first person to consider such a possibility was Katok ([Kat1]). In this article the entropy is thought of as a dynamical invariant which actually is suggested by its name. More precisely, let us define this dynamical invariant, which is called the topological entropy: let (M, d) be a compact metric space and ψt, a flow on it, we define

.

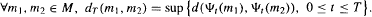Type
Survey Article
Information
Ergodic Theory and Dynamical Systems , Volume 16 , Issue 4 , August 1996 , pp. 623 - 649
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Bab]Babenko, Y.. Closed geodesies, asymptotic volume, and characteristics of group growth. Math. USSR Izv. 33 (1989), 1–37.CrossRefGoogle Scholar
[BCG0]Besson, G., Courtois, G. and Gallot, S.. Le volume et l'entropie minimal des espaces localement symétriques. Invent. Math. 103 (1991), 417–445.CrossRefGoogle Scholar
[BCG1]Besson, G., Courtois, G. and Gallot, S.. Entropies et rigidités des espaces localement symétriques de courbure strictement négative. G.A.F.A. 5(5) (1995), 731–799.Google Scholar
[BCG2]Besson, G., Courtois, G. and Gallot, S.. Les variétés hyperboliques sont des minima locaux de l'entropie topologique. Invent. Math. 117 (1994), 403–445.CrossRefGoogle Scholar
[BCG3]Besson, G., Courtois, G. and Gallot, S.. Entropie et rigidité des espaces localement symétriques de volume fini. In preparation.Google Scholar
[BCG4]Besson, G., Courtois, G. and Gallot, S.. Un lemme de Schwarz réel et applications. In preparation.Google Scholar
[BCG5]Besson, G., Courtois, G. and Gallot, S.. Sur l'entropie des quotients de produits d'espaces symétriques de rang un. In preparation.Google Scholar
[BFL]Benoist, Y., Foulon, P. and Labourie, F.. Flots d'Anosov à distributions stable et instable différentiables. J. Am. Math. Soc. 5(1) (1992), 33–74.Google Scholar
[BK]Burns, K. and Katok, A.. Manifolds with non-positive curvature. Ergod. Th. & Dynam. Sys. 5 (1985), 307–317.CrossRefGoogle Scholar
[BM]Burger, M. and Mozes, S.. CAT(−1) spaces, divergence groups and their commensurators. Preprint, 1995.CrossRefGoogle Scholar
[BP]Benedetti, R. and Petronio, C.. Lectures on hyperbolic geometry (Universitext). Springer, Berlin, 1992.CrossRefGoogle Scholar
[CBY]Yue, Cheng Bo. The ergodic theory of discrete isometry groups on manifolds of variable negative curvature. Preprint, Penn State University.CrossRefGoogle Scholar
[CrK]Croke, Ch. and Kleiner, B.. Conjugacy and rigidity for manifolds with a parallel vector field. J. Diff. Geom. 39(3) (1994), 659–980.Google Scholar
[Cro]Croke, Ch.. Rigidity for surfaces of non-positive curvature. Comm. Math. Helv. 65(1) (1990), 150–169.CrossRefGoogle Scholar
[DE]Douady, A. and Earle, C.. Conformally natural extensions of homeomorphisms of the circle. Acta Math. Soc. 27 (1992), 139–142.Google Scholar
[Din]Dinaburg, E. I.. On the relations among various entropy characteristics of dynamical systems. Math. USSR Izv. 5 (1971), 337–378.CrossRefGoogle Scholar
[EL]Eells, J. and Lemaire, L.. A report on harmonic maps. Bull. London Math. Soc. 10 (1978), 1–68.CrossRefGoogle Scholar
[Fed]Federer, H.. Geometric Measure Theory (Grundlehren Band 153). Springer, Berlin, 1969.Google Scholar
[FL]Foulon, P. and Labourie, F.. Sur les variétés compactes asymptotiquement harmoniques. Invent. Math. 109 (1992), 97–111.CrossRefGoogle Scholar
[Fla]Flaminio, L.. Local entropy rigidity for hyperbolic manifolds. Preprint, March 1994.Google Scholar
[Fur]Furstenberg, H.. A Poisson formula for semi-simple Lie groups. Ann. Math. 77 (1963), 335–386.CrossRefGoogle Scholar
[Ghy]Ghys, E.. Flots d'Anosov dont les feuilletages stables sont différentiables. Ann. Sci. École Norm. Sup. 20 (1987), 251–270.CrossRefGoogle Scholar
[Gro1]Gromov, M.. Volume and bounded cohomology. Publ. Math. Inst. Hautes Étud. Sci. 56 (1981), 213–307.Google Scholar
[Gro2]Gromov, M.. Filling Riemannian manifolds. J. Diff. Geom. 18 (1983), 1–147.Google Scholar
[Kai]Kaimanovitch, V.. Invariant measures of the geodesic flow and measures at infinity on negatively curved manifolds. Ann. Inst. Henri Poincaré 53(4) (1990), 361–393.Google Scholar
[Kat1]Katok, A.. Entropy and closed geodesies. Ergod. Th. & Dynam. Sys. 2 (1982), 339–367.CrossRefGoogle Scholar
[Kat2]Katok, A.. Four applications of conformal equivalence to geometry and dynamics. Ergod. Th. & Dynam. Sys. 8 (1988), 139–152.Google Scholar
[Kni]Knieper, G.. Spherical means on compact Riemannian manifolds of negative curvature. Diff. Geom. Appl. 4 (1994), 361–390.CrossRefGoogle Scholar
[Led]Ledrappier, F.. Harmonic measures and Bowen—Margulis measures. Israel J. Math. 71 (1990), 275–287.CrossRefGoogle Scholar
[Man]Manning, A.. Topological entropy for geodesic flows. Ann. Math. 110 (1979), 567–573.CrossRefGoogle Scholar
[Mar]Margulis, G. A.. Applications of ergodic theory to the investigation of manifolds of negative curvature. Funct. Anal. Appl. 3 (1969), 335–336.CrossRefGoogle Scholar
[Mos]Mostow, G. D.. Quasiconformal mappings in n-space and the rigidity of hyperbolic space forms. Publ. Math. Inst. Hautes Étud. Sci. 34 (1968), 53–104.CrossRefGoogle Scholar
[Nic]Nichols, P. J.. The ergodic theory of discrete groups. London Math. Soc. Lecture note ser. 143 (1989).Google Scholar
[Ot]Otal, J.-P.. Le spectre marqué des longueurs des surfaces à courbure négative. Ann. Math. 131 (1990) 151–162.CrossRefGoogle Scholar
[Pat]Patterson, S. J.. The limit set of a Fuchsian group. Acta Math. 136 (1976), 241–273.CrossRefGoogle Scholar
[Pes]Pesin, Y.. Equations for the entropy of a geodesic flow on a compact Riemannian manifold without focal points. Math. Notes 24 (1978), 796–805.CrossRefGoogle Scholar
[Rob]Robert, G.. Invariants topologiques et géométriques reliés aux longueurs des géodésiques et aux sections harmoniques de fibrés. Thèse de Doctoral. L'Université de Grenoble I, 1994.Google Scholar
[Sam]Sambusetti, A.. In preparation.Google Scholar
[Sul]Sullivan, D.. The density at infinity of a discrete group of hyperbolic motions. Publ. Math. Inst. Hautes Étud. Sci. 50 (1979), 171–202.CrossRefGoogle Scholar
[Ver]Vérovic, P.. Entropie et métriques de Finsler. In preparation.Google Scholar
[Wal]Walters, P.. An Introduction to Ergodic Theory (Graduate Text in Maths 79). Springer, Berlin, 1982.CrossRefGoogle Scholar