Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T14:42:19.010Z Has data issue: false hasContentIssue false
  • English
  • Français

Measure rigidity for algebraic bipermutative cellular automata

Published online by Cambridge University Press:  01 December 2007

MATHIEU SABLIK
MATHIEU SABLIK*
Affiliation:
Institut de Mathématiques de Luminy, UMR 6206-Campus de Luminy, Case 907, 13288 Marseille Cedex 09, France (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 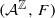be a bipermutative algebraic cellular automaton. We present conditions that force a probability measure, which is invariant for the 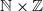-action of F and the shift map σ, to be the Haar measure on Σ, a closed shift-invariant subgroup of the abelian compact group 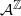. This generalizes simultaneously results of Host et al (B. Host, A. Maass and S. Martínez. Uniform Bernoulli measure in dynamics of permutative cellular automata with algebraic local rules. Discrete Contin. Dyn. Syst. 9(6) (2003), 1423–1446) and Pivato (M. Pivato. Invariant measures for bipermutative cellular automata. Discrete Contin. Dyn. Syst. 12(4) (2005), 723–736). This result is applied to give conditions which also force an (F,σ)-invariant probability measure to be the uniform Bernoulli measure when F is a particular invertible affine expansive cellular automaton on .

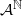Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 27 , Issue 6 , December 2007 , pp. 1965 - 1990
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Arnaudiès, J.-M. and Bertin, J.. Groupes, Algèbres et Géométrie, Tome 1. Ellipses, Paris, 1993.Google Scholar
[2]Boyle, M. and Maass, A.. Expansive invertible onesided cellular automata. J. Math. Soc. Japan 52(4) (2000), 725–740.CrossRefGoogle Scholar
[3]Dartnell, P., Maass, A. and Schwartz, F.. Combinatorial constructions associated to the dynamics of one-sided cellular automata. Theoret. Comput. Sci. 304(1–3) (2003), 485–497.CrossRefGoogle Scholar
[4]Einsiedler, M.. Isomorphism and measure rigidity for algebraic actions on zero-dimensional groups. Monatsh. Math. 144(1) (2005), 39–69.CrossRefGoogle Scholar
[5]Ferrari, P. A., Maass, A., Martínez, S. and Ney, P.. Cesàro mean distribution of group automata starting from measures with summable decay. Ergod. Th. & Dynam. Sys. 20(6) (2000), 1657–1670.CrossRefGoogle Scholar
[6]Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Systems Theory 1 (1967), 1–49.CrossRefGoogle Scholar
[7]Guichardet, A.. Analyse Harmonique Commutative (Monographies Universitaires de Mathématiques, 26). Dunod, Paris, 1968.Google Scholar
[8]Hedlund, G. A.. Endormorphisms and automorphisms of the shift dynamical system. Math. Systems Theory 3 (1969), 320–375.CrossRefGoogle Scholar
[9]Host, B., Maass, A. and Martínez, S.. Uniform Bernoulli measure in dynamics of permutative cellular automata with algebraic local rules. Discrete Contin. Dyn. Syst. 9(6) (2003), 1423–1446.CrossRefGoogle Scholar
[10]Kitchens, B. P.. Expansive dynamics on zero-dimensional groups. Ergod. Th. & Dynam. Sys. 7(2) (1987), 249–261.CrossRefGoogle Scholar
[11]Lang, S.. Algebra, 3rd edn.(Graduate Texts in Mathematics, 211). Springer, New York, 2002.CrossRefGoogle Scholar
[12]Ledrappier, F.. Un champ markovien peut être d’entropie nulle et mélangeant. C. R. Acad. Sci. Paris Sér. A–B 287(7) (1978), A561–A563.Google Scholar
[13]Lind, D. A.. Applications of ergodic theory and sofic systems to cellular automata. Phys. D 10(1–2) (1984), 36–44.CrossRefGoogle Scholar
[14]Maass, A. and Martínez, S.. On Cesàro limit distribution of a class of permutative cellular automata. J. Stat. Phys. 90(1–2) (1998), 435–452.CrossRefGoogle Scholar
[15]Petersen, K.. Ergodic Theory (Cambridge Studies in Advanced Mathematics, 2). Cambridge University Press, Cambridge, 1989. Corrected reprint of the 1983 original.Google Scholar
[16]Pivato, M.. Invariant measures for bipermutative cellular automata. Discrete Contin. Dyn. Syst. 12(4) (2005), 723–736.CrossRefGoogle Scholar
[17]Pivato, M. and Yassawi, R.. Limit measures for affine cellular automata. Ergod. Th. & Dynam. Sys. 22(4) (2002), 1269–1287.CrossRefGoogle Scholar
[18]Pivato, M. and Yassawi, R.. Limit measures for affine cellular automata. II. Ergod. Th. & Dynam. Sys. 24(6) (2004), 1961–1980.CrossRefGoogle Scholar
[19]Schmidt, K.. Dynamical Systems of Algebraic Origin (Progress in Mathematics, 128). Birkhäuser, Basel, 1995.Google Scholar
[20]Shereshevsky, M. A.. Lyapunov exponents for one-dimensional cellular automata. J. Nonlinear Sci. 2(1) (1992), 1–8.CrossRefGoogle Scholar
[21]Silberger, S.. Subshifts of the three dot system. Ergod. Th. & Dynam. Sys. 25(5) (2005), 1673–1687.CrossRefGoogle Scholar
[22]Tisseur, P.. Cellular automata and Lyapunov exponents. Nonlinearity 13(5) (2000), 1547–1560.CrossRefGoogle Scholar
[23]Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, New York, 1982.CrossRefGoogle Scholar
[24]Ward, T. B.. Additive cellular automata and volume growth. Entropy 2(3) (2000), 142–167 (electronic).CrossRefGoogle Scholar