Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T11:01:18.710Z Has data issue: false hasContentIssue false
  • English
  • Français

Measurable rigidity for Kleinian groups

Published online by Cambridge University Press:  01 June 2015

WOOJIN JEON  and
KEN’ICHI OHSHIKA
WOOJIN JEON
Affiliation:
School of Mathematics, KIAS, Hoegiro 87, Dongdaemun-gu, Seoul, 130-722, Korea email [email protected]
KEN’ICHI OHSHIKA
Affiliation:
Department of Mathematics, Graduate School of Science, Osaka University, Toyonaka, Osaka 560-0043, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 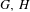$G,H$ be two Kleinian groups with homeomorphic quotients 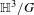$\mathbb{H}^{3}/G$ and 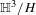$\mathbb{H}^{3}/H$ . We assume that $G$ is of divergence type, and consider the Patterson–Sullivan measures of 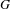$G$ and 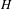$H$ . The measurable rigidity theorem by Sullivan and Tukia says that a measurable and essentially directly measurable equivariant boundary map 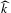$\widehat{k}$ from the limit set $\unicode[STIX]{x1D6EC}_{G}$ of 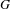$G$ to that of 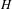$H$ is either the restriction of a Möbius transformation or totally singular. In this paper, we shall show that such 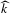$\widehat{k}$ always exists. In fact, we shall construct 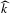$\widehat{k}$ concretely from the Cannon–Thurston maps of 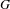$G$ and 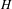$H$ .

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 8 , December 2016 , pp. 2498 - 2511
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agol, I.. Tameness of hyperbolic 3-manifolds. Preprint, 2004, arXiv:math.GT/0405568.Google Scholar
Anderson, J., Falk, K. and Tukia, P.. Conformal measures associated to ends of hyperbolic n-manifolds. Q. J. Math. 58 (2007), 1–15.CrossRefGoogle Scholar
Beardon, A.. The exponent of convergence of Poincaré series. Proc. Lond. Math. Soc. (3) 18 (1968), 461–483.CrossRefGoogle Scholar
Bishop, C. J. and Jones, P. W.. The law of iterated logarithm for Kleinian groups. Contemp. Math. 211 (1997), 17–50.CrossRefGoogle Scholar
Bonahon, F.. Bout des variétés hyperboliques de dimension 3. Ann. of Math. (2) 124 (1986), 71–158.CrossRefGoogle Scholar
Brock, J., Canary, D. and Minsky, Y.. The classification of Kleinian surface groups II: the ending lamination conjecture. Ann. of Math. (2) 176 (2012), 1–149.Google Scholar
Burger, M. and Mozes, S.. CAT(–1)-spaces, divergence groups and their commensurators. J. Amer. Math. Soc. 9(1) (1996), 57–93.Google Scholar
Calegari, D. and Gabai, D.. Shrinkwrapping and the taming of hyperbolic 3-manifolds. J. Amer. Math. Soc. 19(2) (2006), 385–446.CrossRefGoogle Scholar
Canary, D.. Ends of hyperbolic 3-manifolds. J. Amer. Math. Soc. 6(1) (1993), 1–35.Google Scholar
Culler, M. and Shalen, P.. Paradoxical decompositions, 2-generator Kleinian groups, and volumes of hyperbolic 3-manifolds. J. Amer. Math. Soc. 5(2) (1992), 231–288.Google Scholar
Feighn, M. and McCullough, D.. Finiteness conditions for 3-manifolds with boundary. Amer. J. Math. 109 (1987), 1155–1169.Google Scholar
Feres, R. and Katok, A.. Ergodic theory and dynamics of G-spaces. Handbook of Dynamical Systems. Vol 1A. Eds. Hasselblatt, B. and Katok, A.. North-Holland, Amsterdam, 2002, pp. 665–763.Google Scholar
Gerasimov, V.. Floyd maps for relatively hyperbolic groups. Geom. Funct. Anal. 22 (2012), 1–39.Google Scholar
Hersonsky, S. and Paulin, F.. On the rigidity of discrete isometry groups of negatively curved spaces. Comment. Math. Helv. 72 (1997), 349–388.CrossRefGoogle Scholar
Jeon, W., Kapovich, I., Leininger, C. and Ohshika, K.. Conical limit points and the Cannon–Thurston map. Preprint, 2014, arXiv:1401.2638.Google Scholar
Lecuire, C.. Plissage des variétés hyperboliques de dimension 3. Invent. Math. 164 (2006), 85–141.Google Scholar
Lecuire, C.. Structure hyperboliques convexes sur les variétés de dimension 3. Thèse, ENS Lyon, 2004.Google Scholar
Minsky, Y. N.. The classification of Kleinian surface groups. I. Models and bounds. Ann. of Math. (2) 171 (2010), 1–107.CrossRefGoogle Scholar
Mj, M.. Cannon–Thurston map for surface groups. Ann. of Math. (2) 179 (2014), 1–80.Google Scholar
Mj, M.. Cannon–Thurston maps for Kleinian groups. Preprint, 2010, arXiv:1002.0996.Google Scholar
Nicholls, P. J.. The Ergodic Theory of Discrete Groups (London Mathematical Society Lecture Note Series, 143) . Cambridge University Press, Cambridge, 1989.Google Scholar
Patterson, S. J.. The limit set of a Fuchsian group. Acta Math. 136 (1976), 241–273.CrossRefGoogle Scholar
Scott, P.. Compact submanifolds of a 3-manifold. J. Lond. Math. Soc. (2) 7 (1973), 246–250.CrossRefGoogle Scholar
Soma, T.. Equivariant, almost homeomorphic maps between S 1 and S 2 . Proc. Amer. Math. Soc. 123(9) (1995), 2915–2920.Google Scholar
Spatzier, R. and Zimmer, R.. Fundamental groups of negatively curved manifolds and actions of semisimple groups. Topology 30 (1991), 591–601.Google Scholar
Srivastava, S. M.. A Course on Borel Sets (Graduate Text in Mathematics, 180) . Springer, New York, 1998.Google Scholar
Sullivan, D.. The density at infinity of a discrete group of hyperbolic motions. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 171–202.Google Scholar
Sullivan, D.. On the ergodic theory at infinity of an arbitrary discrete group of hyperbolic motions. Riemann Surfaces and Related Topics: Proceeding of the 1978 Stony Brook Conference (Annals of Mathematics Studies, 97) . Princeton University Press, Princeton, NJ, 1981, pp. 465–496.Google Scholar
Sullivan, D.. Discrete conformal groups and measurable dynamics. Bull. Amer. Math. Soc. (N.S.) 6 (1982), 57–73.Google Scholar
Sullivan, D.. Entropy, Hausdorff measures old and new, and limit sets of geometrically finite Kleinian groups. Acta Math. 153 (1984), 259–277.Google Scholar
Thurston, W. P.. The Geometry and Topology of 3-Manifolds (Princeton University Lecture Notes) . 1980, available at http://library.msri.org/nonmsri/gt3m/.Google Scholar
Tukia, P.. A rigidity theorem for Mobius groups. Invent. Math. 97 (1989), 405–431.CrossRefGoogle Scholar
Yue, C.. Mostow rigidity of rank 1 discrete groups with ergodic Bowen–Margulis measure. Invent. Math. 125 (1996), 75–102.Google Scholar
Zimmer, R.. Ergodic Theory and Semi-simple Groups. Birkhäuser, Boston, MA, 1984.Google Scholar