Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T01:02:47.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal absolutely continuous invariant measures for piecewise linear Markov transformations

Published online by Cambridge University Press:  19 September 2008

W. Byers ,
P. Góra  and
A. Boyarsky
W. Byers
Affiliation:
Department of Mathematics, Concordia University, 7141 Sherbrooke Street West, Montreal H4B 1R6, Canada
P. Góra
Affiliation:
Department of Mathematics, Warsaw University, Warszawa, Poland
A. Boyarsky
Affiliation:
Department of Mathematics, Concordia University, 7141 Sherbrooke Street West, Montreal H4B 1R6, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 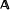be an irreducible 0–1 matrix such that the non-zero entries in each row are consecutive. Let 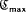be the class of piecewise linear Markov transformations τ on [0, 1] into [0, 1] induced by 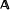for which the absolutely continuous invariant measure has maximal entropy. The main result presents necessary and sufficient slope conditions on τ which guarantee that τ ∈ .

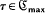Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 10 , Issue 4 , December 1990 , pp. 645 - 656
Copyright
Copyright © Cambridge University Press 1990

References

REFERENCES

[1]Walters, P.. Ruelle's operator theorem and g-measures. Trans. Amer. Math. Soc. 214 (1975), 375–387.Google Scholar
[2]Ledrappier, F.. Some properties of absolutely continuous invariant measures on the interval. Ergod. Th. & Dynam. Sys. 1 (1981), 77–93.CrossRefGoogle Scholar
[3]Proppe, H., Byers, W. & Boyarsky, A.. Singularity of topological conjugacies between certain unimodal maps of the interval. Israel J. Math. 44 (1983), 277–288.CrossRefGoogle Scholar
[4]Byers, W. & Boyarsky, A.. Absolutely continuous invariant measures that are maximal. Trans. Amer. Math. Soc. 290 (1985), 303–314.Google Scholar
[5]Byers, W. & Boyarsky, A.. A graph theoretic bound on the number of independent absolutely continuous invariant measures. J. Math. Anal. Appl. 139 (1989), 139–151.Google Scholar
[6]Hofbauer, F.. β-shifts have unique maximal measure. Monatsh. Math. 85 (1978), 189–198.CrossRefGoogle Scholar
[7]Hofbauer, F.. Maximal measures for piecewise monotonically increasing functions on [0, 1]. In: Lecture Notes in Math. 729, Springer, Berlin and New York (1979), 66–77.Google Scholar
[8]Hofbauer, F.. On intrinsic ergodicity of piecewise monotonic transformations with positive entropy. Israel J. Math. 34 (1979), 213–237.CrossRefGoogle Scholar
[9]Misiurewicz, M.. Absolutely continuous measures for certain maps of an interval. Publ. Math. IHES 53 (1981), 17–52.CrossRefGoogle Scholar
[10]Lasota, A. & Yorke, J. A.. On the existence of invariant measures for piecewise monotonic transformations. Trans. Amer. Math. Soc. 186 (1974), 481–488.CrossRefGoogle Scholar
[11]Bowen, R.. Invariant measures for Markov maps of the interval. Comm. Math. Phys. 69 (1979), 1–17.CrossRefGoogle Scholar
[12]Parry, W.. Intrinsic Markov chains. Trans Amer. Math. Soc. 112 (1964), 55–65.CrossRefGoogle Scholar
[13]Walters, P.. An Introduction to Ergodic Theory. Springer-Verlag, New York (1982).CrossRefGoogle Scholar