Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:52:41.380Z Has data issue: false hasContentIssue false
  • English
  • Français

Marked length rigidity for Fuchsian buildings

Published online by Cambridge University Press:  13 March 2018

DAVID CONSTANTINE  and
JEAN-FRANÇOIS LAFONT
DAVID CONSTANTINE
Affiliation:
Wesleyan University, Mathematics and Computer Science Department, Middletown, CT 06459, USA email [email protected]
JEAN-FRANÇOIS LAFONT
Affiliation:
Department of Mathematics, Ohio State University, Columbus, OH 43210, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider finite $2$-complexes 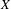$X$ that arise as quotients of Fuchsian buildings by subgroups of the combinatorial automorphism group, which we assume act freely and cocompactly. We show that locally CAT(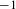$-1$) metrics on 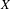$X$, which are piecewise hyperbolic and satisfy a natural non-singularity condition at vertices, are marked length spectrum rigid within certain classes of negatively curved, piecewise Riemannian metrics on 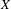$X$. As a key step in our proof, we show that the marked length spectrum function for such metrics determines the volume of 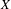$X$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 12 , December 2019 , pp. 3262 - 3291
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aplerin, R. and Bass, H.. Length functions of group actions on 𝜆-trees. Combinatorial Group Theory and Topology (Alta, Utah, 1984) (Annals of Mathematics Studies, 111) . Princeton University Press, Princeton, NJ, 1987, pp. 265–378.Google Scholar
Ballmann, W. and Brin, M.. Orbihedra of nonpositive curvature. Publ. Math. Inst. Hautes Études Sci. 82 (1995), 169–209.Google Scholar
Billingsley, P.. Convergence of Probability Measures. Wiley, New York, 1968.Google Scholar
Bankovic, A. and Leininger, C.. Marked-length-spectral rigidity for flat metrics. Trans. Amer. Math. Soc. 370 (2018), 1867–1884.Google Scholar
Bonahon, F.. The geometry of Teichmüller space via geodesic currents. Invent. Math. 92 (1988), 139–162.Google Scholar
Bonahon, F.. Geodesic currents on negatively curved groups. Arboreal Group Theory (Mathematical Sciences Research Institute Publications, 19) . Ed. Alperin, Roger C.. Springer, New York, 1991, pp. 143–168.Google Scholar
Bourdon, M.. Sur le birapport au bord des CAT(- 1)-espaces. Publ. Math. Inst. Hautes Études Sci. 83 (1996), 95–104.Google Scholar
Bourdon, M.. Immeubles hyperboliques, dimension conforme, et rigidité de Mostow. Geom. Funct. Anal. 7 (1997), 245–268.Google Scholar
Bourdon, M.. Sur les immeubles Fuchsiens et leur type de quasi-isométrie. Ergod. Th. & Dynam. Sys. 20 (2000), 343–364.Google Scholar
Bourdon, M. and Pajot, H.. Rigidity of quasi-isometries for some hyperbolic buildings. Comment. Math. Helv. 75 (2000), 701–736.Google Scholar
Brown, K. S.. Buildings. Springer, New York, 1989.Google Scholar
Croke, C. B. and Dairbekov, N. S.. Lengths and volumes in Riemannian manifolds. Duke Math. J. 125(1) (2004), 1–14.Google Scholar
Cornfeld, I. P., Fomin, S. V. and Sinai, Ya. G.. Ergodic Theory. Springer, New York, 1982.Google Scholar
Constantine, D. and Lafont, J.-F.. Marked length rigidity for one dimensional spaces. J. Topol. Anal., to appear, available at arXiv:1209.3709.Google Scholar
Culler, M. and Morgan, J. W.. Group actions on ℝ-trees. Proc. Lond. Math. Soc. 55 (1987), 571–604.Google Scholar
Constantine, D.. Marked length spectrum rigidity in nonpositive curvature with singularities. Indiana Univ. Math. J. (2017), to appear, available at https://www.iumj.indiana.edu/IUMJ/Preprints/7545.pdf.Google Scholar
Croke, C.. Rigidity for surfaces of nonpositive curvature. Comment. Math. Helv. 65(1) (1990), 150–169.Google Scholar
Dal’Bo, F. and Kim, I.. Marked length rigidity for symmetric spaces. Comment. Math. Helv. 77 (2002), 399–407.Google Scholar
Daskalopoulos, G., Mese, C. and Vdovina, A.. Superrigidity of hyperbolic buildings. Geom. Funct. Anal. 21 (2011), 905–919.Google Scholar
Fanaï, H.-R.. Comparaison des volumes des variétés Riemanniennes. C. R. Math. Acad. Sci. Paris 339 (2004), 199–201.Google Scholar
Feit, W. and Higman, G.. The nonexistence of certain generalized polygons. J. Algebra 1 (1964), 114–131.Google Scholar
Hamenstädt, U.. Entropy-rigidity of locally symmetric spaces of negative curvature. Ann. Math. 131(2) (1990), 35–51.Google Scholar
Hersonsky, S. and Paulin, F.. On the rigidity of discrete isometry groups of negatively curved spaces. Comment. Math. Helv. 72 (1997), 349–388.Google Scholar
Ledrappier, F. and Lim, S.-H.. Volume entropy for hyperbolic buildings. J. Mod. Dyn. 4 (2010), 139–165.Google Scholar
Otal, J.-P.. Le spectre marqué des longueurs des surfaces à courbure négative. Ann. Math. 131(1) (1990), 151–160.Google Scholar
Otal, J.-P.. Sur la géométrie symplectique de l’espace des géodésiques d’une variété à courbure négative. Rev. Mat. Iberoam. 8 (1992), 441–456.Google Scholar
Payne, S. E. and Thas, J. A.. Finite Generalized Quadrangles. European Mathematical Society, Zurich, 2009.Google Scholar
Santaló, L. A.. Integral Geometry and Geometric Probability. Cambridge University Press, Cambridge, 2004.Google Scholar
Sun, Z.. Marked length spectra and areas of non-positively curved cone metrics. Geom. Dedicata 178 (2015), 189–194.Google Scholar
van Maldeghem, H.. Generalized Polygons. Birkhäuser, Basel, 1998.Google Scholar
Weiss, R. M.. The Structure of Spherical Buildings. Princeton University Press, Princeton, NJ, 2003.Google Scholar
Xie, X.. Quasi-isometric rigidity of Fuchsian buildings. Topology 45 (2006), 101–169.Google Scholar