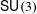Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Burelle, Jean-Philippe
and
Lawton, Sean
2022.
Dynamics on nilpotent character varieties.
Conformal Geometry and Dynamics of the American Mathematical Society,
Vol. 26,
Issue. 10,
p.
194.
González-Prieto, Ángel
Martínez, Javier
and
Muñoz, Vicente
2023.
Geometry of SU(3)-character varieties of torus knots.
Topology and its Applications,
Vol. 339,
Issue. ,
p.
108586.
Forni, Giovanni
Goldman, William M.
Lawton, Sean
and
Matheus, Carlos
2024.
Non-ergodicity on SU(2) and SU(3) character varieties of the once-punctured torus.
Annales Henri Lebesgue,
Vol. 7,
Issue. ,
p.
1099.
Thomas, Cigole
2025.
Asymptotic dynamics on character varieties over finite fields.
Geometriae Dedicata,
Vol. 219,
Issue. 2,