Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T14:55:36.383Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower and upper bounds for the Lyapunov exponents of twisting dynamics: a relationship between the exponents and the angle of Oseledets’ splitting

Published online by Cambridge University Press:  17 April 2012

M.-C. ARNAUD
M.-C. ARNAUD*
Affiliation:
Laboratoire d’Analyse non linéaire et Géométrie (EA 2151), Université d’Avignon et des Pays de Vaucluse, F-84 018 Avignon, France (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider locally minimizing measures for conservative twist maps of the 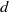$d$-dimensional annulus and for Tonelli Hamiltonian flows defined on a cotangent bundle 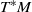$T^*M$. For weakly hyperbolic measures of such type (i.e. measures with no zero Lyapunov exponents), we prove that the mean distance/angle between the stable and unstable Oseledets bundles gives an upper bound on the sum of the positive Lyapunov exponents and a lower bound on the smallest positive Lyapunov exponent. We also prove some more precise results.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 3 , June 2013 , pp. 693 - 712
Copyright
Copyright © 2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Arnaud, M.-C.. Fibrés de Green et régularité des graphes $C^0$-Lagrangiens invariants par un flot de Tonelli. Ann. Henri Poincaré 9(5) (2008), 881–926.CrossRefGoogle Scholar
[2]Arnaud, M.-C.. Three results on the regularity of the curves that are invariant by an exact symplectic twist map. Publ. Math. Inst. Hautes Études Sci. 109 (2009), 1–17.Google Scholar
[3]Arnaud, M.-C.. The link between the shape of the Aubry–Mather sets and their Lyapunov exponents. Preprint, 2009, arXiv:0902.3266.Google Scholar
[4]Arnaud, M.-C.. Green bundles, Lyapunov exponents and regularity along the supports of the minimizing measures. Ann. of Math. (2) 174(3) (2011), 1571–1601.Google Scholar
[5]Arnol’d, V. I.. Mathematical Methods of Classical Mechanics, 2nd edn(Graduate Texts in Mathematics, 60). Springer, New York, 1989, translated from the Russian by K. Vogtmann and A. Weinstein.Google Scholar
[6]Bialy, M. and MacKay, R.. Symplectic twist maps without conjugate points. Israel J. Math. 141 (2004), 235–247.Google Scholar
[7]Contreras, G. and Iturriaga, R.. Convex Hamiltonians without conjugate points. Ergod. Th. & Dynam. Sys. 19(4) (1999), 901–952.CrossRefGoogle Scholar
[8]Fathi, A.. Weak KAM Theorems in Lagrangian Dynamics, book in preparation.Google Scholar
[9]Foulon, P.. Estimation de l’entropie des systèmes lagrangiens sans points conjugués. Ann. Inst. H. Poincaré Phys. Théor. 57(2) (1992), 117–146.Google Scholar
[10]Freire, A. and Mañé, R.. On the entropy of the geodesic flow in manifolds without conjugate points. Invent. Math. 69(3) (1982), 375–392.Google Scholar
[11]Golé, C.. Symplectic twist maps. Global variational techniques. Adv. Ser. Nonlinear Dynam. 18 (2001).Google Scholar
[12]Green, L. W.. A theorem of E. Hopf. Michigan Math. J. 5 (1958), 31–34.Google Scholar
[13]Iturriaga, R.. A geometric proof of the existence of the Green bundles. Proc. Amer. Math. Soc. 130(8) (2002), 2311–2312.Google Scholar
[14]Ledrappier, F.. Quelques propriétés des exposants caractéristiques (in French) [Some properties of characteristic exponents]. École d’étéde probabilités de Saint-Flour, XII-1982 (Lecture Notes in Mathematics, 1097). Springer, Berlin, 1984, pp. 305–396.Google Scholar
[15]Mather, J. N.. Action minimizing invariant measures for positive definite Lagrangian systems. Math. Z. 207(2) (1991), 169–207.Google Scholar