No CrossRef data available.
Published online by Cambridge University Press: 28 September 2020
Let f be a germ of a holomorphic diffeomorphism with an irrationally indifferent fixed point at the origin in
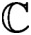 ${\mathbb C}$
(i.e.
${\mathbb C}$
(i.e.
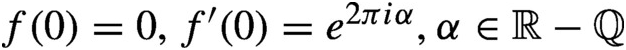 $f(0) = 0, f'(0) = e^{2\pi i \alpha }, \alpha \in {\mathbb R} - {\mathbb Q}$
). Pérez-Marco [Fixed points and circle maps. Acta Math.179(2) (1997), 243–294] showed the existence of a unique continuous monotone one-parameter family of non-trivial invariant full continua containing the fixed point called Siegel compacta, and gave a correspondence between germs and families
$f(0) = 0, f'(0) = e^{2\pi i \alpha }, \alpha \in {\mathbb R} - {\mathbb Q}$
). Pérez-Marco [Fixed points and circle maps. Acta Math.179(2) (1997), 243–294] showed the existence of a unique continuous monotone one-parameter family of non-trivial invariant full continua containing the fixed point called Siegel compacta, and gave a correspondence between germs and families
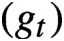 $(g_t)$
of circle maps obtained by conformally mapping the complement of these compacts to the complement of the unit disk. The family of circle maps
$(g_t)$
of circle maps obtained by conformally mapping the complement of these compacts to the complement of the unit disk. The family of circle maps
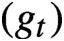 $(g_t)$
is the orbit of a locally defined semigroup
$(g_t)$
is the orbit of a locally defined semigroup
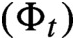 $(\Phi _t)$
on the space of analytic circle maps, which we show has a well-defined infinitesimal generator X. The explicit form of X is obtained by using the Loewner equation associated to the family of hulls
$(\Phi _t)$
on the space of analytic circle maps, which we show has a well-defined infinitesimal generator X. The explicit form of X is obtained by using the Loewner equation associated to the family of hulls
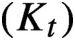 $(K_t)$
. We show that the Loewner measures
$(K_t)$
. We show that the Loewner measures
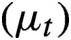 $(\mu _t)$
driving the equation are 2-conformal measures on the circle for the circle maps
$(\mu _t)$
driving the equation are 2-conformal measures on the circle for the circle maps
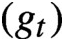 $(g_t)$
.
$(g_t)$
.