Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T16:06:16.434Z Has data issue: false hasContentIssue false
  • English
  • Français

Local unstable entropies of partially hyperbolic diffeomorphisms

Part of: Measure-theoretic ergodic theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  26 February 2019

WEISHENG WU
WEISHENG WU*
Affiliation:
Department of Applied Mathematics, College of Science, China Agricultural University, Beijing, 100083, PR China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a 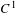$C^{1}$-partially hyperbolic diffeomorphism 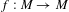$f:M\rightarrow M$. Following the ideas in establishing the local variational principle for topological dynamical systems, we introduce the notions of local unstable metric entropies (and local unstable topological entropy) relative to a Borel cover 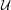${\mathcal{U}}$ of 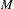$M$. It is shown that they coincide with the unstable metric entropy (and unstable topological entropy, respectively), when 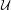${\mathcal{U}}$ is an open cover with small diameter. We also define the unstable tail entropy in the sense of Bowen and the unstable topological conditional entropy in the sense of Misiurewicz, and demonstrate that both of them vanish. Some generalizations of these results to the case of unstable pressure are also investigated.

Keywords

partial hyperbolicitylocal variational principlelocal unstable entropylocal unstable pressure

MSC classification

Primary: 37D30: Partially hyperbolic systems and dominated splittings
Secondary: 37D35: Thermodynamic formalism, variational principles, equilibrium states 28D20: Entropy and other invariants
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 8 , August 2020 , pp. 2274 - 2304
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barreira, L. and Pesin, Ya B.. Nonuniform Hyperbolicity: Dynamics of Systems with Nonzero Lyapunov Exponents (Encyclopedia of Mathematics and its Applications, 115). Cambridge University Press, Cambridge, 2007.CrossRefGoogle Scholar
Blanchard, F., Glasner, E. and Host, B.. A variation on the variational principle and applications to entropy pairs. Ergod. Th. & Dynam. Sys. 17(1) (1997), 29–43.CrossRefGoogle Scholar
Bowen, R.. Entropy-expansive maps. Trans. Amer. Math. Soc. 164 (1972), 323–331.CrossRefGoogle Scholar
Boyle, M., Fiebig, D. and Fiebig, U.. Residual entropy, conditional entropy and subshift covers. Forum Math. 14(5) (2002), 713–757.CrossRefGoogle Scholar
Climenhaga, V. and Katok, A.. Measure theory through dynamical eyes. Preprint, 2012, arXiv:1208.4550.Google Scholar
Downarowicz, T.. Entropy in Dynamical Systems (New Mathematical Monographs, 18), 1st edn. Cambridge University Press, Cambridge, 2011.CrossRefGoogle Scholar
Downarowicz, T. and Serafin, J.. Fiber entropy and conditional variational principles in compact non-metrizable spaces. Fund. Math. 172 (2002), 217–247.CrossRefGoogle Scholar
Glasner, E. and Weiss, B.. On the interplay between measurable and topological dynamics. Handbook of Dynamical Systems, Vol. 1B. Eds. Hasselblatt, B. and Katok, A.. North-Holland, Amsterdam, 2005, pp. 597–648.Google Scholar
Goodman, T. N. T.. Relating topological entropy and measure entropy. Bull. Lond. Math. Soc. 3(2) (1971), 176–180.CrossRefGoogle Scholar
Goodwyn, L. W.. Topological entropy bounds measure-theoretic entropy. Proc. Amer. Math. Soc. 23(3) (1969), 679–688.CrossRefGoogle Scholar
Hu, H., Hua, Y. and Wu, W.. Unstable entropies and variational principle for partially hyperbolic diffeomorphisms. Adv. Math. 321 (2017), 31–68.CrossRefGoogle Scholar
Hu, H., Wu, W. and Zhu, Y.. Unstable pressure and u-equilibrium states for partially hyperbolic diffeomorphisms. Preprint, 2017, arXiv:1710.02816.CrossRefGoogle Scholar
Huang, W. and Ye, X.. A local variational relation and applications. Israel J. Math. 151(1) (2006), 237–279.CrossRefGoogle Scholar
Huang, W., Ye, X. and Zhang, G.. A local variational principle for conditional entropy. Ergod. Th. & Dynam. Sys. 26(1) (2006), 219–245.CrossRefGoogle Scholar
Huang, W. and Yi, Y.. A local variational principle of pressure and its applications to equilibrium states. Israel J. Math. 161(1) (2007), 29–74.CrossRefGoogle Scholar
Ledrappier, F. and Strelcyn, J.-M.. A proof of the estimation from below in Pesin’s entropy formula. Ergod. Th. & Dynam. Sys. 2(2) (1982), 203–219.CrossRefGoogle Scholar
Ledrappier, F. and Walters, P.. A relativised variational principle for continuous transformations. J. Lond. Math. Soc. 16(2) (1977), 568–576.CrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms: part I: characterization of measures satisfying Pesin’s entropy formula. Ann. of Math. (2) 122 (1985), 509–539.CrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms: part II: relations between entropy, exponents and dimension. Ann. of Math. (2) 122 (1985), 540–574.CrossRefGoogle Scholar
Ma, X. and Chen, E.. Variational principles for relative local pressure with subadditive potentials. J. Math. Phys. 54(3) (2013), 2701, 25 pp.CrossRefGoogle Scholar
Ma, X., Chen, E. and Zhang, A.. A relative local variational principle for topological pressure. Sci. China Math. 53(6) (2010), 1491–1506.CrossRefGoogle Scholar
Misiurewicz, M.. Topological conditional entropy. Studia Math. 55(2) (1976), 175–200.CrossRefGoogle Scholar
Misiurewicz, M.. A short proof of the variational principle for a ℤ+n action on a compact space. Astérisque 40 (1976), 227–262.Google Scholar
Pesin, Ya. B. and Sinai, Ya. G.. Gibbs measures for partially hyperbolic attractors. Ergod. Th. & Dynam. Sys. 2(3–4) (1982), 417–438.CrossRefGoogle Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. A. and Ures, R.. Accessibility and stable ergodicity for partially hyperbolic diffeomorphisms with 1d-center bundle. Invent. Math. 172(2) (2008), 353–381.CrossRefGoogle Scholar
Rohlin, V. A.. On the fundamental ideas of measure theory. Amer. Math. Soc. Transl. 71 (1952), 55 pp.Google Scholar
Romagnoli, P.. A local variational principle for the topological entropy. Ergod. Th. & Dynam. Sys. 23(05) (2003), 1601–1610.CrossRefGoogle Scholar
Tahzibi, A. and Yang, J.. Invariance principle and rigidity of high entropy measures. Trans. Amer. Math. Soc. 371(2) (2019), 1231–1251.CrossRefGoogle Scholar
Yang, J.. Entropy along expanding foliations. Preprint, 2016, arXiv:1601.05504.Google Scholar
Zhang, G.. Variational principles of pressure. Discrete Contin. Dyn. Syst. 24(4) (2009), 1409–1435.CrossRefGoogle Scholar