Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T17:57:08.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Local limit theorems in relatively hyperbolic groups I: rough estimates

Part of: Special aspects of infinite or finite groups Limit theorems Probabilistic methods in group theory

Published online by Cambridge University Press:  23 March 2021

MATTHIEU DUSSAULE
MATTHIEU DUSSAULE*
Affiliation:
LMPT, Université de Tours, Parc de Grandmont, 37200Tours, France
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This is the first of a series of two papers dealing with local limit theorems in relatively hyperbolic groups. In this first paper, we prove rough estimates for the Green function. Along the way, we introduce the notion of relative automaticity which will be useful in both papers and we show that relatively hyperbolic groups are relatively automatic. We also define the notion of spectral positive recurrence for random walks on relatively hyperbolic groups. We then use our estimates for the Green function to prove that 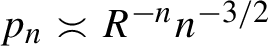$p_n\asymp R^{-n}n^{-3/2}$ for spectrally positive-recurrent random walks, where 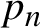$p_n$ is the probability of going back to the origin at time n and where R is the inverse of the spectral radius of the random walk.

Keywords

random walksrelative hyperbolicitylocal limitTauberian theory

MSC classification

Primary: 60F15: Strong theorems 20F65: Geometric group theory
Secondary: 20F67: Hyperbolic groups and nonpositively curved groups 20P05: Probabilistic methods in group theory
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 6 , June 2022 , pp. 1926 - 1966
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0), which permits unrestricted re-use, distribution and reproduction, provided the original article is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Antolín, Y. and Ciobanu, L.. Finite generating sets of relatively hyperbolic groups and applications to geodesic languages. Trans. Amer. Math. Soc. 368 (2016), 7965–8010.CrossRefGoogle Scholar
Behrstock, J., Druţu, C. and Mosher, L.. Thick metric spaces, relative hyperbolicity, and quasi-isometric rigidity. Math. Ann. 344 (2009) 543–595.CrossRefGoogle Scholar
Bingham, N., Goldie, C. and Teugels, J.. Regular Variation. Cambridge University Press, Cambridge, 1987.CrossRefGoogle Scholar
Blachère, S. and Brofferio, S.. Internal diffusion limited aggregation on discrete groups having exponential growth. Probab. Theory Related Fields 137 (2007), 323–343.CrossRefGoogle Scholar
Bowditch, B.. Geometrical finiteness for hyperbolic groups. J. Funct. Anal. 113 (1993), 245–317.CrossRefGoogle Scholar
Bowditch, B.. Geometrical finiteness with variable negative curvature. Duke Math. J. 77 (1995), 229–274.CrossRefGoogle Scholar
Bowditch, B.. Relatively hyperbolic groups. Internat. J. Algebra Comput. 22 (2012), 1–66.CrossRefGoogle Scholar
Candellero, E. and Gilch, L.. Phase transitions for random walk asymptotics on free products of groups. Random Structures Algorithms 40 (2012), 150–181.CrossRefGoogle Scholar
Cannon, J.. The theory of negatively curved spaces and groups. Ergodic Theory, Symbolic Dynamics and Hyperbolic Spaces. Oxford University Press, Oxford, 1991, pp. 315–369.Google Scholar
Cartwright, D.. Some examples of random walks on free products of discrete groups. Ann. Mat. Pura Appl. 151 (1988), 1–15.CrossRefGoogle Scholar
Cartwright, D.. On the asymptotic behaviour of convolution powers of probabilities on discrete groups. Monatsh. Math. 107 (1989) 287–290.CrossRefGoogle Scholar
Coornaert, M., Delzant, T. and Papadopoulos, A.. Les groupes hyperboliques de Gromov. Géométrie et Théorie des Groupes (Lecture Notes in Mathematics, 1441). Springer, Berlin, 1990.CrossRefGoogle Scholar
Dal’bo, F., Otal, J.-P. and Peigné, M.. Séries de Poincaré des groupes géométriquement finis. Israel J. Math. 118 (2000), 109–124.CrossRefGoogle Scholar
Druţu, C. and Sapir, M.. Tree graded spaces and asymptotic cones of groups. Topology 44 (2005), 959–1058, with an Appendix by Denis Osin and Mark Sapir.CrossRefGoogle Scholar
Dussaule, M. and Gekhtman, I.. Stability phenomena for Martin boundaries of relatively hyperbolic groups. Probab. Theory Related Fields to appear. Preprint, 2019, arXiv:1909.01577.CrossRefGoogle Scholar
Farb, B.. Relatively hyperbolic and automatic groups with applications to negatively curved manifolds. PhD Thesis, Princeton University, 1994.Google Scholar
Farb, B.. Relatively hyperbolic groups. Geom. Funct. Anal. 8 (1998) 810–840.CrossRefGoogle Scholar
Gerasimov, V. and Potyagailo, L.. Quasiconvexity in the relatively hyperbolic groups. J. Reine Angew. Math. 710 (2016), 95–135.Google Scholar
Gerl, P.. A local central limit theorem on some groups. The First Pannonian Symposium on Mathematical Statistics (Lecture Notes in Statistics, 8). Springer, Berlin, 1981, pp. 73–82.Google Scholar
Gerl, P. and Woess, W.. Local limits and harmonic functions for nonisotropic random walks on free groups. Probab. Theory Related Fields 71 (1986), 341–355.CrossRefGoogle Scholar
Ghys, É. and de la Harpe, P.. Sur les Groupes Hyperboliques d’après Mikhael Gromov. Birkhäuser, Boston, MA, 1990.CrossRefGoogle Scholar
Gouëzel, S.. Local limit theorem for symmetric random walks in Gromov-hyperbolic groups. J. Amer. Math. Soc. 27 (2014), 893–928.CrossRefGoogle Scholar
Gouëzel, S. and Lalley, S.. Random walks on co-compact Fuchsian groups. Ann. Sci. Éc. Norm. Supér. 46 (2013), 129–173.Google Scholar
Guivarc’h, Y.. Sur la loi des grands nombres et le rayon spectral d’une marche aléatoire. Conference on Random Walks (Astérisque, 74). Société Mathématique de France, Paris, 1980, pp. 47–98.Google Scholar
Hruska, G.. Relative hyperbolicity and relative quasiconvexity for countable groups. Algebr. Geom. Topol. 10 (2010), 1807–1856.CrossRefGoogle Scholar
Kwaśnicki, M.. Weak version of Karamata’s Tauberian theorem. MathOverflow, https://mathoverflow.net/q/354036 (version: 2020-03-03).Google Scholar
Lalley, S.. Finite range random walk on free groups and homogeneous trees. Ann. Probab. 21 (1993), 2087–2130.CrossRefGoogle Scholar
Maher, J. and Tiozzo, G.. Random walks on weakly hyperbolic groups. J. Reine Angew. Math. 742 (2018), 187–239.CrossRefGoogle Scholar
Masur, H. and Minsky, Y.. Geometry of the complex of curves I: hyperbolicity. Invent. Math. 138 (1999), 103–149.CrossRefGoogle Scholar
Neumann, W. and Shapiro, M.. Automatic structures, rational growth, and geometrically finite hyperbolic groups. Invent. Math. 120 (1995), 259–287.CrossRefGoogle Scholar
Osin, D.. Relatively Hyperbolic Groups: Intrinsic Geometry, Algebraic Properties, and Algorithmic Problems (Memoirs of the American Mathematical Society, 179). American Mathematical Society, Providence, RI, 2006.Google Scholar
Patterson, S.. The limit set of a Fuchsian group. Acta Math. 136 (1976), 241–273.CrossRefGoogle Scholar
Rebbechi, D.. Algorithmic properties of relatively hyperbolic groups. PhD Thesis, Graduate School-Newark Rutgers, The State University of New Jersey, 2001.Google Scholar
Roblin, T.. Ergodicité et équidistribution en courbure négative. Mém. Soc. Math. Fr. 95 (2003), 1–96.Google Scholar
Sisto, A.. Projections and relative hyperbolicity. Enseign. Math. 59 (2013), 165–181.CrossRefGoogle Scholar
Sullivan, D.. Entropy, Hausdorff measures old and new, and limit sets of geometrically finite Kleinian groups. Acta Math. 153 (1984), 259–277.CrossRefGoogle Scholar
Woess, W.. Nearest neighbour random walks on free products of discrete groups. Boll. Unione Mat. Ital. 5-B (1986) 961–982.Google Scholar
Woess, W.. Random Walks on Infinite Graphs and Groups. Cambridge University Press, Cambridge, 2000.CrossRefGoogle Scholar
Yang, W.. Patterson–Sullivan measures and growth of relatively hyperbolic groups. Peking Math. J. to appear. Preprint, 2013, arXiv:1308.6326.Google Scholar
Yang, W.. Statistically convex-cocompact actions of groups with contracting elements. Int. Math. Res. Not. 2019 (2019), 7259–7323.CrossRefGoogle Scholar