Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-16T20:19:53.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Limits of geodesic push-forwards of horocycle invariant measures

Part of: Noncompact transformation groups Riemann surfaces Low-dimensional topology Ergodic theory

Published online by Cambridge University Press:  23 October 2020

GIOVANNI FORNI
GIOVANNI FORNI*
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

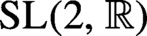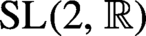We prove several general conditional convergence results on ergodic averages for horocycle and geodesic subgroups of any continuous $\operatorname {SL}(2, \mathbb {R})$ -action on a locally compact space. These results are motivated by theorems of Eskin, Mirzakhani and Mohammadi on the $\operatorname {SL}(2, \mathbb {R})$ -action on the moduli space of Abelian differentials. By our argument we can derive from these theorems an improved version of the ‘weak convergence’ of push-forwards of horocycle measures under the geodesic flow and a short proof of weaker versions of theorems of Chaika and Eskin on Birkhoff genericity and Oseledets regularity in almost all directions for the Teichmüller geodesic flow.

Keywords

Teichmüller horocycle flowpointwise equidistributionBirkhoff ergodic theoremOseledets multiplicative ergodic theorem

MSC classification

Primary: 37A30: Ergodic theorems, spectral theory, Markov operators 30F60: Teichmüller theory
Secondary: 22F30: Homogeneous spaces 57M60: Group actions in low dimensions
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 9 , September 2021 , pp. 2782 - 2804
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bonatti, C., Eskin, A., and Wilkinson, A.. Projective cocycles over $\mathrm{SL}\left(2,\mathbb{R}\right)$ actions: measures invariant under the upper triangular group. Some Aspects of the Theory of Dynamical Systems: A Tribute to Jean-Christophe Yoccoz. Vol. I. Eds. Crovisier, S., Krikorian, R., Matheus, and, C. Senti, S.. Astérisque 415 (2020), 157–180.CrossRefGoogle Scholar
Bainbridge, M., Smillie, J., and Weiss, B.. Horocycle dynamics: new invariants and eigenform loci in the stratum $H\left(1,1\right)$ . Preprint, arXiv:1603.00808.Google Scholar
Chaika, J. and Eskin, A.. Every flat surface is Birkhoff and Oseledets generic in almost every direction. J. Mod. Dyn. 9 (2015), 1–23.CrossRefGoogle Scholar
Eskin, A. and Mirzakhani, M.. Invariant and stationary measures for the $\mathrm{SL}\left(2,\mathbb{R}\right)$ action on moduli space. Publ. Math. Inst. Hautes Études Sci. 127(1) (2018), 95–324.CrossRefGoogle Scholar
Eskin, A. and Masur, H.. Pointwise asymptotic formulas on flat surfaces. Ergod. Th. & Dynam. Sys. 21(2) (2001), 443–478.CrossRefGoogle Scholar
Eskin, A., Mirzakhani, M., and Mohammadi, A.. Isolation, equidistribution, and orbit closures for the $\mathrm{SL}\left(2,\mathbb{R}\right)$ action on moduli space. Ann. Math. 182 (2015), 673–721.CrossRefGoogle Scholar
Filip, S.. Semisimplicity and rigidity of the Kontsevich–Zorich cocycle. Invent. Math. 205(3) (2016), 617–670.CrossRefGoogle Scholar
Forni, G., Matheus, C., and Zorich, A.. Lyapunov spectrum of invariant sub-bundles of the Hodge bundle. Ergod. Th. & Dynam. Sys. 34(2) (2012), 353–408.CrossRefGoogle Scholar
Forni, G.. Deviation of ergodic averages for area-preserving flows on surfaces of higher genus. Ann. Math. 155(1) (2002), 1–103.CrossRefGoogle Scholar
Khalil, O.. Pointwise equidistribution and translates of measures on homogeneous spaces. Ergod. Th. & Dynam. Sys. 40(2) (2020), 453–477.CrossRefGoogle Scholar
Minsky, Y. and Weiss, B.. Nondivergence of horocyclic flows on moduli space. J. Reine Angew. Math. (Crelle’s J.) 552 (2002), 131–177.Google Scholar
Veech, W.. Siegel measures. Ann. Math. 148(3) (1998), 895–944.CrossRefGoogle Scholar