Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T13:08:13.026Z Has data issue: false hasContentIssue false
  • English
  • Français

Lifting mixing properties by Rokhlin cocycles

Published online by Cambridge University Press:  08 November 2011

MARIUSZ LEMAŃCZYK  and
FRANÇOIS PARREAU
MARIUSZ LEMAŃCZYK
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, 12/18 Chopin Street, 87–100 Toruń, Poland (email: [email protected])
FRANÇOIS PARREAU
Affiliation:
Laboratoire d’Analyse, Géométrie, et Applications, UMR 7539, Université Paris 13 et CNRS, 99, av. J.-B. Clément, 93430 Villetaneuse, France (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the problem of lifting various mixing properties from a base automorphism T∈Aut(X,ℬ,μ) to skew products of the form Tφ,𝒮, where φ:X→G is a cocycle with values in a locally compact Abelian group G, 𝒮=(Sg)g∈G is a measurable representation of G in Aut(Y,𝒞,ν) and Tφ,𝒮 acts on the product space (X×Y,ℬ⊗𝒞,μ⊗ν) by 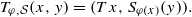It is also shown that whenever T is ergodic (mildly mixing, mixing) but Tφ,𝒮 is not ergodic (is not mildly mixing, not mixing), then, on a non-trivial factor 𝒜⊂𝒞 of 𝒮, the corresponding Rokhlin cocycle x↦Sφ(x) ∣𝒜 is a coboundary (a quasi-coboundary).

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 32 , Issue 2: Daniel J. Rudolph – in Memoriam , April 2012 , pp. 763 - 784
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aaronson, J.. An Introduction to Infinite Ergodic Theory (Mathematical Surveys and Monographs, 50). American Mathematical Society, Providence, RI, 1997.CrossRefGoogle Scholar
[2]Abramov, L. M. and Rokhlin, V. A.. The entropy of a skew product of measure preserving transformation. Amer. Math. Soc. Transl. 48 (1965), 225–245.Google Scholar
[3]Anzai, H.. Ergodic skew product transformation on the torus. Osaka J. Math. 3 (1951), 83–99.Google Scholar
[4]Austin, T. and Lemańczyk, M.. Relatively finite measure-preserving extensions and lifting multipliers by Rokhlin cocycles. J. Fixed Point Theory Appl. 6(1) (2009), 115–131.CrossRefGoogle Scholar
[5]Danilenko, A. and Lemańczyk, M.. A class of multipliers for 𝒲⊥. Israel J. Math. 148 (2005), 137–168.CrossRefGoogle Scholar
[6]Foguel, S. R.. The Ergodic Theory of Markov Processes. Van Nostrand, New York, 1969.Google Scholar
[7]Furstenberg, H.. Strict ergodicity and transformations of the torus. Amer. J. Math. 83 (1961), 573–601.CrossRefGoogle Scholar
[8]Furstenberg, H.. Disjointness in ergodic theory, minimal sets and diophantine approximation. Math. Syst. Theory 1 (1967), 1–49.CrossRefGoogle Scholar
[9]Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.CrossRefGoogle Scholar
[10]Furstenberg, H. and Weiss, B.. The finite multipliers of infinite ergodic transformations. Lecture Notes in Math. 668 (1978), 127–132.CrossRefGoogle Scholar
[11]Glasner, E.. On the multipliers of 𝒲⊥. Ergod. Th. & Dynam. Sys. 14 (1994), 129–140.CrossRefGoogle Scholar
[12]Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101). American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
[13]Glasner, E. and Weiss, B.. Processes disjoint from weak mixing. Trans. Amer. Math. Soc. 316 (1989), 689–703.CrossRefGoogle Scholar
[14]Glasner, S.. Proximal flows. Lecture Notes in Math. 517 (1976).Google Scholar
[15]Hahn, F. and Parry, W.. Some characteristic properties of dynamical systems with quasi-discrete spectra. Math. Systems Theory 2 (1968), 179–190.CrossRefGoogle Scholar
[16]Hamachi, T. and Osikawa, M.. Ergodic groups of automorphisms and Krieger’s theorems. Sem. Math. Sci. 3 (1991).Google Scholar
[17]Host, B., Méla, J.-F. and Parreau, F.. Analyse Harmonique des mesures (Astérisque, 135–136). Soc. Math. France, Paris, 1986.Google Scholar
[18]Host, B., Méla, J.-F. and Parreau, F.. Non-singular transformations and spectral analysis of measures. Bull. Soc. Math. France 119 (1991), 33–90.CrossRefGoogle Scholar
[19]Katok, A. B.. Cocycles, cohomology and combinatorial constructions in ergodic theory. Proc. Symp. Pure Math. 69 (2001), 107–173, in collaboration with E. A. Robinson Jr.CrossRefGoogle Scholar
[20]Katok, A. and Thouvenot, J.-P.. Spectral Properties and Combinatorial Constructions in Ergodic Theory (Handbook of Dynamical Systems, 1B). Elsevier B. V., Amsterdam, 2006, pp. 649–743.Google Scholar
[21]Lemańczyk, M.. Spectral Theory of Dynamical Systems (Encyclopedia of Complexity and System Science, 19). Springer, Berlin, 2009, pp. 8554–8575.Google Scholar
[22]Lemańczyk, M. and Lesigne, E.. Ergodicity of Rokhlin cocycles. J. Anal. Math. 85 (2001), 43–86.CrossRefGoogle Scholar
[23]Lemańczyk, M. and Parreau, F.. Rokhlin extensions and lifting disjointness. Ergod. Th. & Dynam. Sys. 23 (2003), 1525–1550.CrossRefGoogle Scholar
[24]Queffélec, M.. Substitution dynamical systems—spectral analysis. Lecture Notes in Math. 1294 (1987).Google Scholar
[25]Robinson, E. A.. A general condition for lifting theorems. Trans. Amer. Math. Soc. 330 (1992), 725–755.CrossRefGoogle Scholar
[26]Rudolph, D.. Classifying isometric extensions of a Bernoulli shift. Israel J. Math. 34 (1978), 36–60.Google Scholar
[27]Rudolph, D.. k-fold mixing lifts to weakly mixing isometric extensions. Ergod. Th. & Dynam. Sys. 5 (1985), 445–447.CrossRefGoogle Scholar
[28]Rudolph, D.. and cocycle extensions and complementary algebras. Ergod. Th. & Dynam. Sys. 6 (1986), 583–599.CrossRefGoogle Scholar
[29]Ryzhikov, V. V.. Joinings, intertwinings operators, factors, and mixing properties of dynamical systems. Russian Acad. Sci. Izv. Math. 42 (1994), 91–114.Google Scholar
[30]Schmidt, K.. Cocycles of Ergodic Transformation Groups (Lecture Notes in Mathematics, 1). MacMillan Co. of India, 1977.Google Scholar
[31]Zimmer, R.. Extensions of ergodic group actions. Illinois J. Math. 20(3) (1976), 373–409.CrossRefGoogle Scholar