Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ponce, G.
and
Tahzibi, A.
2014.
Central Lyapunov exponent of partially hyperbolic diffeomorphisms of 𝕋³.
Proceedings of the American Mathematical Society,
Vol. 142,
Issue. 9,
p.
3193.
Potrie, Rafael
2014.
A Few Remarks on Partially Hyperbolic Diffeomorphisms of $${\mathbb T}^3$$ T 3 Isotopic to Anosov.
Journal of Dynamics and Differential Equations,
Vol. 26,
Issue. 3,
p.
805.
Hammerlindl, A.
and
Potrie, R.
2014.
Pointwise partial hyperbolicity in three-dimensional nilmanifolds.
Journal of the London Mathematical Society,
Vol. 89,
Issue. 3,
p.
853.
Fisher, Todd
Potrie, Rafael
and
Sambarino, Martín
2014.
Dynamical coherence of partially hyperbolic diffeomorphisms of tori isotopic to Anosov.
Mathematische Zeitschrift,
Vol. 278,
Issue. 1-2,
p.
149.
Tahzibi, Ali
and
Gogolev, Andrey
2015.
Center Lyapunov exponents in partially hyperbolic dynamics.
Journal of Modern Dynamics,
Vol. 8,
Issue. 3/4,
p.
549.
Hammerlindl, Andy
and
Potrie, Rafael
2015.
Classification of partially hyperbolic diffeomorphisms in 3-manifolds with solvable fundamental group.
Journal of Topology,
Vol. 8,
Issue. 3,
p.
842.
Hammerlindl, Andy
2015.
On expanding foliations.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 46,
Issue. 3,
p.
407.
Gan, Shaobo
Shi, Yi
and
Zheng, Rusong
2015.
Rotation set of torus homeomorphisms preserving minimal foliations.
Dynamical Systems,
Vol. 30,
Issue. 4,
p.
426.
Potrie, Rafael
2015.
Partial hyperbolicity and foliations in $\mathbb{T}^3$.
Journal of Modern Dynamics,
Vol. 9,
Issue. 01,
p.
81.
Varão, R.
2015.
Lyapunov exponents and smooth invariant foliations for partially hyperbolic diffeomorphisms on.
Dynamical Systems,
Vol. 30,
Issue. 2,
p.
189.
Saghin, Radu
and
Yang, Jiagang
2016.
Continuity of topological entropy for perturbation of time-one maps of hyperbolic flows.
Israel Journal of Mathematics,
Vol. 215,
Issue. 2,
p.
857.
VARÃO, RÉGIS
2016.
Center foliation: absolute continuity, disintegration and rigidity.
Ergodic Theory and Dynamical Systems,
Vol. 36,
Issue. 1,
p.
256.
Micena, F.
2017.
New Derived from Anosov Diffeomorphisms with Pathological Center Foliation.
Journal of Dynamics and Differential Equations,
Vol. 29,
Issue. 3,
p.
1159.
Ren, Yan
Gan, Shao Bo
and
Zhang, Peng Fei
2017.
Accessibility and homology bounded strong unstable foliation for Anosov diffeomorphisms on 3-torus.
Acta Mathematica Sinica, English Series,
Vol. 33,
Issue. 1,
p.
71.
Ponce, G.
Tahzibi, A.
and
Varão, R.
2018.
On the Bernoulli property for certain partially hyperbolic diffeomorphisms.
Advances in Mathematics,
Vol. 329,
Issue. ,
p.
329.
VARÃO, RÉGIS
2018.
Rigidity for partially hyperbolic diffeomorphisms.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 8,
p.
3188.
CARRASCO, PABLO D.
RODRIGUEZ-HERTZ, FEDERICO
RODRIGUEZ-HERTZ, JANA
and
URES, RAÚL
2018.
Partially hyperbolic dynamics in dimension three.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 8,
p.
2801.
HAMMERLINDL, ANDY
and
POTRIE, RAFAEL
2018.
Partial hyperbolicity and classification: a survey.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 2,
p.
401.
URES, RAÚL
and
VÁSQUEZ, CARLOS H.
2018.
On the non-robustness of intermingled basins.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 1,
p.
384.
Saghin, Radu
and
Yang, Jiagang
2019.
Lyapunov exponents and rigidity of Anosov automorphisms and skew products.
Advances in Mathematics,
Vol. 355,
Issue. ,
p.
106764.
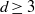 $d\geq 3$ has stable and unstable foliations which are quasi-isometric on the universal cover, and its centre direction is one-dimensional, then the diffeomorphism is leaf conjugate to a linear toral automorphism. In other words, the hyperbolic structure of the diffeomorphism is exactly that of a linear, and thus simple to understand, example. In particular, every partially hyperbolic diffeomorphism on the 3-torus is leaf conjugate to a linear toral automorphism.
$d\geq 3$ has stable and unstable foliations which are quasi-isometric on the universal cover, and its centre direction is one-dimensional, then the diffeomorphism is leaf conjugate to a linear toral automorphism. In other words, the hyperbolic structure of the diffeomorphism is exactly that of a linear, and thus simple to understand, example. In particular, every partially hyperbolic diffeomorphism on the 3-torus is leaf conjugate to a linear toral automorphism.