Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:43:54.142Z Has data issue: false hasContentIssue false
  • English
  • Français

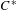KMS states on the $C^{\ast }$-algebras of reducible graphs

Published online by Cambridge University Press:  11 August 2014

ASTRID AN HUEF ,
MARCELO LACA ,
IAIN RAEBURN  and
AIDAN SIMS
ASTRID AN HUEF
Affiliation:
Department of Mathematics and Statistics, University of Otago, PO Box 56, Dunedin 9054, New Zealand email [email protected], [email protected]
MARCELO LACA
Affiliation:
Department of Mathematics and Statistics, University of Victoria, Victoria, Canada BC V8W 3P4 email [email protected]
IAIN RAEBURN
Affiliation:
Department of Mathematics and Statistics, University of Otago, PO Box 56, Dunedin 9054, New Zealand email [email protected], [email protected]
AIDAN SIMS
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, NSW 2522, Australia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the dynamics on the $C^{\ast }$-algebras of finite graphs obtained by lifting the gauge action to an action of the real line. Enomoto, Fujii and Watatani [KMS states for gauge action on 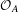${\mathcal{O}}_{A}$. Math. Japon.29 (1984), 607–619] proved that if the vertex matrix of the graph is irreducible, then the dynamics on the graph algebra admits a single Kubo–Martin–Schwinger (KMS) state. We have previously studied the dynamics on the Toeplitz algebra, and explicitly described a finite-dimensional simplex of KMS states for inverse temperatures above a critical value. Here we study the KMS states for graphs with reducible vertex matrix, and for inverse temperatures at and below the critical value. We prove a general result which describes all the KMS states at a fixed inverse temperature, and then apply this theorem to a variety of examples. We find that there can be many patterns of phase transition, depending on the behaviour of paths in the underlying graph.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 8 , December 2015 , pp. 2535 - 2558
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bates, T., Pask, D., Raeburn, I. and Szymański, W.. The C ∗ -algebras of row-finite graphs. New York J. Math. 6 (2000), 307–324.Google Scholar
Carlsen, T. M. and Larsen, N. S.. Partial actions and KMS states on relative graph $C^{\ast }$-algebras. Preprint arXiv:1311.0912.Google Scholar
Enomoto, M., Fujii, M. and Watatani, Y.. KMS states for gauge action on 𝓞A. Math. Japon. 29 (1984), 607–619.Google Scholar
Exel, R. and Laca, M.. Partial dynamical systems and the KMS condition. Comm. Math. Phys. 232 (2003), 223–277.CrossRefGoogle Scholar
Fowler, N. J. and Raeburn, I.. The Toeplitz algebra of a Hilbert bimodule. Indiana Univ. Math. J. 48 (1999), 155–181.CrossRefGoogle Scholar
an Huef, A., Laca, M., Raeburn, I. and Sims, A.. KMS states on the C ∗ -algebras of finite graphs. J. Math. Anal. Appl. 405 (2013), 388–399.CrossRefGoogle Scholar
an Huef, A., Laca, M., Raeburn, I. and Sims, A.. KMS states on C ∗ -algebras associated to higher-rank graphs. J. Funct. Anal. 266 (2014), 265–283.CrossRefGoogle Scholar
Ireland, K. and Rosen, M.. A Classical Introduction to Modern Number Theory (Graduate Texts in Mathematics, 84), 2nd edn. Springer, New York, 1990.CrossRefGoogle Scholar
Kajiwara, T. and Watatani, Y.. KMS states on finite-graph C ∗ -algebras. Kyushu J. Math. 67 (2013), 83–104.CrossRefGoogle Scholar
Kumjian, A. and Pask, D.. Higher rank graph C ∗ -algebras. New York J. Math. 6 (2000), 1–20.Google Scholar
Kumjian, A., Pask, D., Raeburn, I. and Renault, J.. Graphs, groupoids and Cuntz–Krieger algebras. J. Funct. Anal. 144 (1997), 505–541.CrossRefGoogle Scholar
Lind, D.. The entropies of topological Markov shifts and a related class of algebraic integers. Ergod. Th. & Dynam. Sys. 4 (1984), 283–300.CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Pask, D., Raeburn, I. and Weaver, N. A.. A family of 2-graphs arising from two-dimensional subshifts. Ergod. Th. & Dynam. Syst. 29 (2009), 1613–1639.CrossRefGoogle Scholar
Raeburn, I.. Graph Algebras (CBMS Regional Conference Series in Mathematics, 103). American Mathematical Society, Providence, RI, 2005.CrossRefGoogle Scholar
Seneta, E.. Non-Negative Matrices and Markov Chains, 2nd edn. Springer, New York, 1981.CrossRefGoogle Scholar
Smith, S. P.. Category equivalences involving graded modules over path algebras of quivers. Adv. Math. 230 (2012), 1780–1810.CrossRefGoogle Scholar
Smith, S. P.. Shift equivalence and a category equivalence involving graded modules over path algebras of quivers. Preprint, arXiv:1108.4994.Google Scholar
Thomsen, K.. KMS weights on groupoid and graph C ∗ -algebras. J. Funct. Anal. 266 (2014), 2959–2988.CrossRefGoogle Scholar
Yang, D.. Type III von Neumann algebras associated with 𝓞𝜃. Bull. Lond. Math. Soc. 44 (2012), 675–686.CrossRefGoogle Scholar