Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:31:09.405Z Has data issue: false hasContentIssue false
  • English
  • Français

The intersections of self-similar and self-affine sets with their perturbations under the weak separation condition

Published online by Cambridge University Press:  08 November 2016

QI-RONG DENG  and
XIANG-YANG WANG
QI-RONG DENG
Affiliation:
Department of Mathematics, Fujian Normal University, Fuzhou 350117, PR China email [email protected], [email protected]
XIANG-YANG WANG
Affiliation:
School of Mathematics, Sun Yat-Sen University, Guang-Zhou 510275, PR China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a self-similar or self-affine iterated function system (IFS), let $\unicode[STIX]{x1D707}$ be the self-similar or self-affine measure and 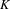$K$ be the self-similar or self-affine set. Assume that the IFS satisfies the weak separation condition and 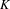$K$ is totally disconnected; then, by using the technique of neighborhood decomposition, we prove that there is a neighborhood 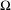$\unicode[STIX]{x1D6FA}$ of the identity map Id such that 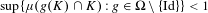$\sup \{\unicode[STIX]{x1D707}(g(K)\cap K):g\in \unicode[STIX]{x1D6FA}\setminus \{\text{Id}\}\}<1$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 4 , June 2018 , pp. 1353 - 1368
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barnsley, M.. Fractals Everywhere, 2nd edn. Academic Press, Boston, MA, 1993.Google Scholar
Barnsley, M. and Vince, A.. Developments in fractal geometry. Bull. Math. Sci. 3 (2013), 299–348.Google Scholar
Deng, Q. R.. Absolute continuity of vector-valued self-affine measures. J. Math. Anal. Appl. 342 (2008), 1250–1264.Google Scholar
Deng, Q. R. and Lau, K. S.. On the equivalence of homogeneous iterated function systems. Nonlinearity 26 (2013), 2767–2775.Google Scholar
Deng, Q. R. and Lau, K. S.. Structure of the class of iterated function systems that generate the same self-similar set. J. Fractal Geom. (2016) to appear.Google Scholar
Deng, Q. R. and Wang, X. Y.. On the boundary of self-affine sets. Abstr. Appl. Anal. 2015 (2015), Article ID 573604, 1–3.Google Scholar
Elekes, M., Keleti, T. and Máthé,  A.. Self-similar and self-affine sets: measure of the intersection of two copies. Ergod. Th. & Dynam. Sys. 30 (2010), 399–440.CrossRefGoogle Scholar
Falconer, K.. The Geometry of Fractal Sets. Cambridge University Press, Cambridge, 1985.Google Scholar
Feng, D. J., Huang, W. and Rao, H.. Affine embeddings and intersections of Cantor sets. J. Math. Pures Appl. (9) 102 (2014), 1062–1079.Google Scholar
Feng, D. J. and Wang, Y.. On the structures of generating iterated function systems of Cantor sets. Adv. Math. 222 (2009), 1964–1981.CrossRefGoogle Scholar
Hutchinson, J.. Fractals and self similarity. Indiana Univ. Math. J. 30 (1981), 713–747.Google Scholar
Honary, B., Moreira, C. G. and Mahdi, P.. Stable intersections of affine Cantor sets. Bull. Braz. Math. Soc. (N.S.) 36 (2005), 363–378.Google Scholar
Lau, K. S. and Ngai, S. M.. Multifractal measures and a weak separation condition. Adv. Math. 141 (1999), 45–96.Google Scholar
Li, J. and Nekka, F.. Intersection of triadic Cantor sets with their translates. II. Hausdorff measure spectrum function and its introduction for the classification of Cantor sets. Chaos Solitons Fractals 19 (2004), 35–46.Google Scholar
Moreira, C. G. T. de A. and Yoccoz, J. C.. Stable intersections of regular Cantor sets with large Hausdorff dimensions. Ann. Math. 154 (2001), 45–96.Google Scholar
Nekka, F. and Li, J.. Intersection of triadic Cantor sets with their translates. I. Fundamental properties. Chaos Solitons Fractals 13 (2002), 1807–1817.CrossRefGoogle Scholar
Peres, Y. and Solomyak, B.. Self-similar measures and intersections of Cantor sets. Trans. Amer. Math. Soc. 350 (1998), 4065–4087.CrossRefGoogle Scholar
Xi, L. F. and Xiong, Y.. Lipschitz equivalence class, ideal class and the Gauss class number problem. Preprint, 2013, arXiv:1304.0103.Google Scholar
Zerner, M.. Weak separation properties for self-similar sets. Proc. Amer. Math. Soc. 124 (1996), 3529–3539.Google Scholar