Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T10:34:37.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrability conditions of geodesic flow on homogeneous Monge manifolds

Published online by Cambridge University Press:  30 September 2013

THIERRY COMBOT  and
THOMAS WATERS
THIERRY COMBOT
Affiliation:
IMCCE, 77 avenue Denfert Rochereau 75014 Paris, France email [email protected]
THOMAS WATERS
Affiliation:
Department of Mathematics, University of Portsmouth, Portsmouth PO1 3HF, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a meromorphic integrability criterion for the geodesic flow of an algebraic manifold of the form 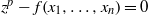${z}^{p} - f({x}_{1} , \ldots , {x}_{n} )= 0$ with the induced metric of 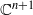${ \mathbb{C} }^{n+ 1} $ and 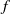$f$ a homogeneous rational function, using a parallel between the properties of such algebraic manifolds and homogeneous potentials. We then apply this criterion to the manifolds of the form 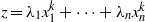$z= {\lambda }_{1} { x}_{1}^{k} + \cdots + {\lambda }_{n} { x}_{n}^{k} $, 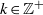$k\in { \mathbb{Z} }^{+ } $, and 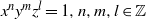${x}^{n} {y}^{m} {z}^{l} = 1, n, m, l\in \mathbb{Z} $, and prove that their geodesic flow is not integrable except for some given exceptional cases.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 1 , February 2015 , pp. 111 - 127
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bolsinov, A. V.. Integrable geodesic flows on Riemannian manifolds. J. Math. Sci. 123 (4) (2004), 4185–4197.Google Scholar
Casale, G., Duval, G., Maciejewski, A. J. and Przybylska, M.. Integrability of Hamiltonian systems with homogeneous potentials of degree zero. Phys. Lett. A 374 (3) (2010), 448–452.Google Scholar
Collins, G. E.. Quantifier elimination for the elementary theory of real closed fields by cylindrical algebraic decomposition. Proc. Int. Conf. Automata Theory and Formal Languages, 2nd GI Conference (Kaiserslautern, 20–23 May 1975) (Lecture Notes in Computer Science, 33). Springer, Berlin, 1975, pp. 134–183.Google Scholar
Craven, B. D.. Complex symmetric matrices. J. Aust. Math. Soc. 10 (3–4) (1969), 341–354.Google Scholar
Davison, C. M. and Dullin, H. R.. Geodesic flow on three dimensional ellipsoids with equal semi-axes. Regul. Chaotic Dyn. 12 (2007), 172–197.Google Scholar
Hietarinta, J.. A search for integrable two-dimensional Hamiltonian systems with polynomial potential. Phys. Lett. A 96 (6) (1983), 273–278.Google Scholar
Hietarinta, J.. Direct methods in the search for a second invariant. Phys. Rep. 147 (2) (1987), 87–154.Google Scholar
Jacobi, C. G. J.. Fundamenta nova theoriae functionum ellipticarum. Bornträger, Königsberg, 1829.Google Scholar
Kimura, T.. On Riemann’s equations which are solvable by quadratures. Funkcial. Ekvac, 12 (1969), 269–281.Google Scholar
Klingenberg, W.. Riemannian Geometry. De Gruyter, Berlin, 1995.Google Scholar
Kozlov, V. V.. Some integrable extensions of Jacobi’s problem of geodesics on an ellipsoid. J. Appl. Math. Mech. 59 (1) (1995), 1–7.Google Scholar
Llibre, J., Mahdi, A. and Valls, C.. Analytic integrability of Hamiltonian systems with a homogeneous polynomial potential of degree four. J. Math. Phys. 52 (1) (2011), 012702.Google Scholar
Llibre, J., Mahdi, A. and Valls, C.. Polynomial integrability of the Hamiltonian systems with homogeneous potential of degree-2. Phys. Lett. A 375 (2011), 1845–1849.Google Scholar
Llibre, J., Mahdi, A. and Valls, C.. Polynomial integrability of the Hamiltonian systems with homogeneous potential of degree-3. Phys. D 240 (2011), 1928–1935.Google Scholar
Maciejewski, A. J. and Przybylska, M.. All meromorphically integrable 2d Hamiltonian systems with homogeneous potential of degree 3. Phys. Lett. A 327 (2004), 461–473.Google Scholar
Maciejewski, A. J. and Przybylska, M.. Darboux points and integrability of Hamiltonian systems with homogeneous polynomial potential. J. Math. Phys. 46 (2005), 0629091.Google Scholar
Maciejewski, A. J., Przybylska, M. and Yoshida, H.. Necessary conditions for super-integrability of Hamiltonian systems. Phys. Lett. A 372 (34) (2008), 5581–5587.Google Scholar
Morales-Ruiz, J. J.. Differential Galois Theory and Non-integrability of Hamiltonian Systems. Birkhäuser, Basel, 1999.Google Scholar
Morales-Ruiz, J. J. and Ramis, J. P.. Galoisian obstructions to integrability in Hamiltonian systems. Methods Appl. Anal. 8 (1) (2001), 33–96.Google Scholar
Morales-Ruiz, J. J. and Ramis, J. P.. Galoisian obstructions to integrability in Hamiltonian systems II. Methods Appl. Anal. 8 (1) (2001), 97–112.Google Scholar
Morales-Ruiz, J. J. and Ramis, J. P.. A note on the non-integrability of some Hamiltonian systems with a homogeneous potential. Methods Appl. Anal. 8 (1) (2001), 113–120.Google Scholar
Nakagawa, K., Maciejewski, A. J. and Przybylska, M.. New integrable Hamiltonian system with first integral quartic in momenta. Phys. Lett. A 343 (2005), 171–173.Google Scholar
Nakagawa, K. and Yoshida, H.. A list of all 2d homogeneous polynomial potentials with a polynomial integral of order at most 4 in the momenta. J. Phys. A: Math. Gen. 34 (2001), 8611.Google Scholar
Przybylska, M.. Darboux points and integrability of Hamiltonian systems with three and more degrees of freedom. Nongeneric cases. Regul. Chaotic Dyn. 14 (3) (2009), 349–388.Google Scholar
Szczesny, J. and Dobrowolski, T.. Geodesic deviation equation approach to chaos. Ann. of Phys. 277 (1999), 161–176.Google Scholar
Tabanov, M. B.. New ellipsoidal confocal coordinates and geodesics on an ellipsoid. J. Math. Sci. 82 (6) (1996), 3851–3858.Google Scholar
Wald, R. M.. General Relativity. University of Chicago Press, Chicago, 1984.CrossRefGoogle Scholar
Wang, Z. X. and Guo, D. R.. Special Functions. World Scientific, Singapore, 1989.Google Scholar
Waters, T. J.. Non-integrability of geodesic flow on certain algebraic surfaces. Phys. Lett. A 376 (17) (2012), 1442–1445.Google Scholar
Waters, T. J.. Regular and irregular geodesics on spherical harmonic surfaces. Phys. D 241 (5) (2012), 543–552.Google Scholar
Yoshida, H.. A criterion for the non-existence of an additional first integral in Hamiltonian systems with a homogeneous potential. Phys. D 29 (1–2) (1987), 128–142.Google Scholar
Yoshida, H.. A new necessary condition for the integrability of Hamiltonian systems with a two-dimensional homogeneous potential. Phys. D 128 (1999), 53–69.Google Scholar