Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:43:08.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Instability of the isolated spectrum for W-shaped maps

Published online by Cambridge University Press:  30 May 2012

ZHENYANG LI  and
PAWEŁ GÓRA
ZHENYANG LI
Affiliation:
Department of Mathematics and Statistics, Concordia University, 1455 de Maisonneuve Blvd West, Montreal, Quebec H3G 1M8, Canada (email: [email protected], [email protected])
PAWEŁ GÓRA
Affiliation:
Department of Mathematics and Statistics, Concordia University, 1455 de Maisonneuve Blvd West, Montreal, Quebec H3G 1M8, Canada (email: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note we consider the W-shaped map 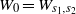$W_0=W_{s_1,s_2}$ with 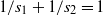${1}/{s_1}+{1}/{s_2}=1$ and show that the eigenvalue 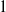$1$ is not stable. We do this in a constructive way. For each perturbing map 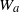$W_a$ we show the existence of a ‘second’ eigenvalue 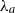$\lambda _a$, such that 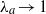$\lambda _a\to 1$ as 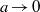$a\to 0$, which proves instability of the isolated spectrum of 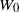$W_0$. At the same time, the existence of second eigenvalues close to 1 causes the maps 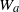$W_a$to behave in a metastable way. There are two almost-invariant sets, and the system spends long periods of consecutive iterations in each of them, with infrequent jumps from one to the other.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 4 , August 2013 , pp. 1052 - 1059
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Boyarsky, A. and Góra, P.. Laws of Chaos: Invariant Measures and Dynamical Systems in One Dimension (Probability and its Applications). Birkhäuser, Boston, MA, 1997.Google Scholar
[2]Eslami, P. and Góra, P.. Stronger Lasota–Yorke inequality for piecewise monotonic transformations. Preprint, available at http://www.peymaneslami.com/EslamiGora_Stronger_LY_Ineq.pdf.Google Scholar
[3]Eslami, P. and Misiurewicz, M.. Singular limits of absolutely continuous invariant measures for families of transitive maps. J. Difference Equ. Appl. 18 (2012), 739–750.Google Scholar
[4]Froyland, G. and Stančević, O.. Escape rates and Perron–Frobenius operators: open and closed dynamical systems. Discrete Contin. Dyn. Syst. Ser. B 14 (2010), 457–472.Google Scholar
[5]Keller, G.. Stochastic stability in some chaotic dynamical systems. Monatsh. Math. 94(4) (1982), 313–333.Google Scholar
[6]Keller, G. and Liverani, C.. Stability of the spectrum for transfer operators. Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 28(1) (1999), 141–152.Google Scholar
[7]Lasota, A. and Yorke, J. A.. On the existence of invariant measures for piecewise monotonic transformations. Trans. Amer. Math. Soc. 186 (1973), 481–488.Google Scholar
[8]Li, Z., Góra, P., Boyarsky, A., Proppe, H. and Eslami, P.. Family of piecewise expanding maps having singular measure as a limit of ACIMs, Ergod. Th. & Dynam. Sys. to appear.Google Scholar
[9]Li, Z.. $W$-like maps with various instabilities of acim’s. Preprint, 2011, arXiv:1109.5199v1.Google Scholar