Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T16:49:03.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Inner amenability for groups and central sequences in factors

Published online by Cambridge University Press:  12 December 2014

IONUT CHIFAN ,
THOMAS SINCLAIR  and
BOGDAN UDREA
IONUT CHIFAN
Affiliation:
Department of Mathematics, University of Iowa, 14 MacLean Hall, IA 52242, USA IMAR, Bucharest, Romania email [email protected]
THOMAS SINCLAIR
Affiliation:
Department of Mathematics, University of California, Los Angeles, Box 951555, Los Angeles, CA 90095-1555, USA email [email protected]
BOGDAN UDREA
Affiliation:
IMAR, Bucharest, Romania email [email protected] Department of Mathematics, University of Illinois, Urbana Champaign, IL 61801, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

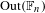We show that a large class of i.c.c., countable, discrete groups satisfying a weak negative curvature condition are not inner amenable. By recent work of Hull and Osin [Groups with hyperbolically embedded subgroups. Algebr. Geom. Topol.13 (2013), 2635–2665], our result recovers that mapping class groups and $\text{Out}(\mathbb{F}_{n})$ are not inner amenable. We also show that the group-measure space constructions associated to free, strongly ergodic p.m.p. actions of such groups do not have property Gamma of Murray and von Neumann [On rings of operators IV. Ann. of Math. (2) 44 (1943), 716–808].

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 4 , June 2016 , pp. 1106 - 1129
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akemann, C. A. and Pedersen, G. K.. Central sequences and inner derivations of separable C ∗ -algebras. Amer. J. Math. 101 (1979), 1047–1061.Google Scholar
Bekka, M. E. B.. Amenable unitary representations of locally compact groups. Invent. Math. 100 (1990), 383–401.Google Scholar
Bestvina, M., Bromberg, K. and Fujiwara, K.. Bounded cohomology via quasi-trees. Preprint, 2013,arXiv:1306.1542(v1).Google Scholar
Brown, N. P. and Ozawa, N.. C∗ -Algebras and Finite-Dimensional Approximations (Graduate Studies in Mathematics, 88). American Mathematical Society, Providence, RI.Google Scholar
Chifan, I. and Sinclair, T.. On the structural theory of II1 factors of negatively curved groups. Ann. Sci. Éc. Norm. Supér. 46 (2013), 1–33.CrossRefGoogle Scholar
Chifan, I., Sinclair, T. and Udrea, B.. On the structural theory of II1 factors of negatively curved groups. II: Actions by product groups. Adv. Math. 245 (2013), 208–236.Google Scholar
Connes, A.. Classification of injective factors Cases II1 , II∞ , III𝜆 , 𝜆≠1. Ann. of Math. (2) 104 (1976), 73–115.CrossRefGoogle Scholar
Dahmani, F., Guirardel, F. and Osin, D.. Hyperbolically embedded subgroups and rotating families in groups acting on hyperbolic spaces. Preprint, 2011, arXiv:11117048(v3).Google Scholar
Effros, E. G.. Property Γ and inner amenability. Proc. Amer. Math. Soc. 47 (1975), 483–486.Google Scholar
Farley, D.. Proper isometric actions of Thompson’s groups on Hilbert space. Int. Math. Res. Not. IMRN 45 (2003), 2409–2414.Google Scholar
Haagerup, U. and Olesen, K. K.. The Thompson groups $T$ and $V$ are not inner-amenable. Preprint, 2014.Google Scholar
Hamenstädt, U.. Bounded cohomology and isometry groups of hyperbolic spaces. J. Eur. Math. Soc. 10 (2008), 315–349.CrossRefGoogle Scholar
de la Harpe, P.. Groupes hyperboliques, algèbres d’opérateurs et un théorème de Jolissaint. C. R. Acad. Sci. Paris Sér. I Math. 307 (1988), 771–774.Google Scholar
de la Harpe, P. and Skandalis, G.. Les réseaux dans les groupes semi-simples ne sont pas intérieurement moyennables. Enseign. Math. 40 (1994), 291–311.Google Scholar
Houdayer, C.. Structure of II1 factors arising from free Bogoljubov actions of arbitrary groups. Adv. Math. 260 (2014), 414–457.Google Scholar
Hull, M. and Osin, D.. Groups with hyperbolically embedded subgroups. Algebr. Geom. Topol. 13 (2013), 2635–2665.CrossRefGoogle Scholar
Jolissaint, P.. Moyennabilite interieure du groupe F de Thompson. C. R. Acad. Sci. Paris, Ser. I 325 (1997), 61–64.Google Scholar
Jolissaint, P.. Central sequences in the factor associated with the Thompsons group F. Ann. Inst. Fourier (Grenoble) 48(4) (1998), 1093–1106.Google Scholar
McDuff, D.. Central sequences and the hyperfinite factor. Proc. Lond. Math. Soc. 21 (1970), 443–461.Google Scholar
Mineyev, I.. Straightening and bounded cohomology of hyperbolic groups. Geom. Funct. Anal. 11 (2001), 807–839.CrossRefGoogle Scholar
Mineyev, I., Monod, N. and Shalom, Y.. Ideal bicombings for hyperbolic groups and applications. Topology 43 (2004), 1319–1344.CrossRefGoogle Scholar
Mineyev, I. and Yaman, A.. Relative hyperbolicity and bounded cohomology. Preprint, 2009.Google Scholar
Murray, F. J. and von Neumann, J.. On rings of operators IV. Ann. of Math. (2) 44 (1943), 716–808.Google Scholar
Ol’shanskii, A.. On the question of the existence of an invariant mean on a group. Uspekhi Mat. Nauk 35 (1980), 199–200.Google Scholar
Ol’shanskii, A. and Sapir, M.. Non-amenable finitely presented torsion-by-cyclic groups. Pub. Math. Inst. Hautes Études Sci. 96(1) (2003), 43–169.Google Scholar
Osin, D.. Acylindrically hyperbolic groups. Preprint, 2013, arXiv:1304.1246(v1).Google Scholar
Ozawa, N.. Solid von Neumann algebras. Acta Math. 192 (2004), 111–117.Google Scholar
Ozawa, N. and Popa, S.. Some prime factorization results for type II1 factors. Invent. Math. 156 (2004), 223–234.Google Scholar
Ozawa, N. and Popa, S.. On a class of II1 factors with at most one Cartan subalgebra. Ann. of Math. (2) 172 (2010), 713–749.CrossRefGoogle Scholar
Ozawa, N. and Popa, S.. On a class of II1 factors with at most one Cartan subalgebra, II. Amer. J. Math. 132 (2010), 841–866.Google Scholar
Peterson, J.. L 2 -rigidity in von Neumann algebras. Invent. Math. 175 (2009), 417–433.Google Scholar
Peterson, J. and Sinclair, T.. On cocycle superrigidity for Gaussian actions. Ergod. Th. & Dynam. Sys. 32 (2012), 249–272.Google Scholar
Peterson, J. and Thom, A.. Group cocycles and the ring of affiliated operators. Invent. Math. 185 (2011), 561–592.Google Scholar
Popa, S.. Strong rigidity of II1 factors arising from malleable actions of w-rigid groups I. Invent. Math. 165 (2006), 369–408.Google Scholar
Popa, S.. Deformation and rigidity for group actions and von Neumann algebras. International Congress of Mathematicians, Vol. I, pp. 445–477. European Mathematical Society, Zürich, 2007.Google Scholar
Popa, S.. On Ozawa’s property for free group factors. Int. Math. Res. Not. IMRN (2007), Art ID rnm036. 10pp.Google Scholar
Popa, S.. On spectral gap rigidity and Connes invariant 𝜒(M). Proc. Amer. Math. Soc. 138 (2010), 3531–3539.Google Scholar
Popa, S. and Vaes, S.. Strong rigidity of generalized Bernoulli actions and computation of their symmetry groups. Adv. Math. 217 (2008), 833–872.Google Scholar
Popa, S. and Vaes, S.. Unique Cartan decomposition for II1 factors arising from arbitrary actions of hyperbolic groups. J. Reine Angew. Math. to appear.Google Scholar
Sakai, S.. Asymptotically abelian II1 factors. Publ. RIMS, Kyoto Univ. Ser. A 4 (1968), 299–307.Google Scholar
Sinclair, T.. Strong solidity of group factors from lattices in SO(n, 1) and SU(n, 1). J. Funct. Anal. 260 (2011), 3209–3221.Google Scholar
Sisto, A.. Contracting elements and random walks. Preprint, 2011, arXiv:1112.2666(v1).Google Scholar
Thom, A.. Low degree bounded cohomology invariants and negatively curved groups. Groups Geom. Dyn. 3 (2009), 343–358.Google Scholar
Tucker-Drob, R. D.. Shift-minimal groups, fixed price 1, and the unique trace property. Preprint, 2012.Google Scholar
Vaes, S.. An inner amenable group whose von Neumann algebra does not have property Gamma. Acta Math. 208 (2012), 389–394.Google Scholar