Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-08T14:31:59.581Z Has data issue: false hasContentIssue false
  • English
  • Français

Inhomogeneous self-similar sets with overlaps

Published online by Cambridge University Press:  04 May 2017

SIMON BAKER ,
JONATHAN M. FRASER  and
ANDRÁS MÁTHÉ
SIMON BAKER
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK email [email protected], [email protected]
JONATHAN M. FRASER
Affiliation:
Mathematical Institute, The University of St Andrews, St Andrews KY16 9SS, UK email [email protected]
ANDRÁS MÁTHÉ
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is known that if the underlying iterated function system satisfies the open set condition, then the upper box dimension of an inhomogeneous self-similar set is the maximum of the upper box dimensions of the homogeneous counterpart and the condensation set. First, we prove that this ‘expected formula’ does not hold in general if there are overlaps in the construction. We demonstrate this via two different types of counterexample: the first is a family of overlapping inhomogeneous self-similar sets based upon Bernoulli convolutions; and the second applies in higher dimensions and makes use of a spectral gap property that holds for certain subgroups of 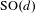$\text{SO}(d)$ for $d\geq 3$. We also obtain new upper bounds, derived using sumsets, for the upper box dimension of an inhomogeneous self-similar set which hold in general. Moreover, our counterexamples demonstrate that these bounds are optimal. In the final section we show that if the weak separation property is satisfied, that is, the overlaps are controllable, then the ‘expected formula’ does hold.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 1 , January 2019 , pp. 1 - 18
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, S.. Approximation properties of 𝛽-expansions. Acta Arith. 168 (2015), 269–287.Google Scholar
Baker, S.. Approximation properties of $\unicode[STIX]{x1D6FD}$ -expansions II. Ergod. Th. & Dynam. Sys. to appear.Google Scholar
Barnsley, M. F. and Demko, S.. Iterated function systems and the global construction of fractals. Proc. R. Soc. Lond. A 399 (1985), 243–275.Google Scholar
Benjamini, I. and Solomyak, B.. Spacings and pair correlations for finite Bernoulli convolutions. Nonlinearity 22 (2009), 381–393.Google Scholar
Drinfeld, V.. Finitely-additive measures on S 2 and S 3 , invariant with respect to rotations. Funct. Anal. Appl. 18 (1984), 245–246.Google Scholar
Falconer, K. J.. Techniques in Fractal Geometry. John Wiley, Chichester, 1997.Google Scholar
Falconer, K. J.. Fractal Geometry: Mathematical Foundations and Applications, 2nd edn. John Wiley, Chichester, 2003.Google Scholar
Fraser, J. M.. On the packing dimension of box-like self-affine sets in the plane. Nonlinearity 25 (2012), 2075–2092.Google Scholar
Fraser, J. M.. Inhomogeneous self-similar sets and box dimensions. Studia Math. 213 (2012), 133–156.Google Scholar
Fraser, J. M.. Inhomogeneous self-affine carpets. Indiana Univ. Math. J. 65 (2016).Google Scholar
Garsia, A.. Arithmetic properties of Bernoulli convolutions. Trans. Amer. Math. Soc. 102 (1962), 409–432.Google Scholar
Hochman, M.. On self-similar sets with overlaps and inverse theorems for entropy. Ann. of Math. (2) 180 (2014), 773–822.Google Scholar
Hochman, M.. On self-similar sets with overlaps and inverse theorems for entropy in $\mathbb{R}^{d}$ . Preprint, 2015, http://arxiv.org/abs/1503.09043.Google Scholar
Lalley, S. P.. The packing and covering functions of some self-similar fractals. Indiana Univ. Math. J. 37 (1989), 699–709.Google Scholar
Margulis, G.. Some remarks on invariant means. Monatsh. Math. 90 (1980), 233–235.Google Scholar
Olsen, L. and Snigireva, N.. L q spectra and Rényi dimensions of in-homogeneous self-similar measures. Nonlinearity 20 (2007), 151–175.Google Scholar
Peres, Y. and Solomyak, B.. Problems on self-similar sets and self-affine sets: an update. Fractal Geometry and Stochastics, II (Greifswald/Koserow, 1998) (Progress in Probability, 46) . Birkhäuser, Basel, 2000, pp. 95–106.Google Scholar
Przytycki, F. and Urbański, M.. On the Hausdorff dimension of some fractal sets. Studia Math. 93 (1989), 155–186.Google Scholar
Snigireva, N.. Inhomogeneous self-similar sets and measures. PhD Dissertation, University of St Andrews, 2008.Google Scholar
Sullivan, D.. For n > 3 there is only one finitely additive rotationally invariant measure on the n-sphere defined on all Lebesgue measurable subsets. Bull. Amer. Math. Soc. 4 (1981), 121–123.+3+there+is+only+one+finitely+additive+rotationally+invariant+measure+on+the+n-sphere+defined+on+all+Lebesgue+measurable+subsets.+Bull.+Amer.+Math.+Soc.+4+(1981),+121–123.>Google Scholar
Zerner, M. P. W.. Weak separation properties for self-similar sets. Proc. Amer. Math. Soc. 124 (1996), 3529–3539.Google Scholar