No CrossRef data available.
Published online by Cambridge University Press: 12 May 2016
Suppose that  $X$ is a Polish space,
$X$ is a Polish space, 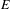 $E$ is a countable Borel equivalence relation on
$E$ is a countable Borel equivalence relation on 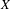 $X$, and
$X$, and  $\unicode[STIX]{x1D707}$ is an
$\unicode[STIX]{x1D707}$ is an 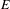 $E$-invariant Borel probability measure on
$E$-invariant Borel probability measure on 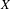 $X$. We consider the circumstances under which for every countable non-abelian free group
$X$. We consider the circumstances under which for every countable non-abelian free group 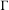 $\unicode[STIX]{x1D6E4}$, there is a Borel sequence
$\unicode[STIX]{x1D6E4}$, there is a Borel sequence 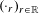 $(\cdot _{r})_{r\in \mathbb{R}}$ of free actions of
$(\cdot _{r})_{r\in \mathbb{R}}$ of free actions of 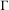 $\unicode[STIX]{x1D6E4}$ on
$\unicode[STIX]{x1D6E4}$ on 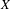 $X$, generating subequivalence relations
$X$, generating subequivalence relations 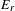 $E_{r}$ of
$E_{r}$ of 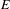 $E$ with respect to which
$E$ with respect to which  $\unicode[STIX]{x1D707}$ is ergodic, with the further property that
$\unicode[STIX]{x1D707}$ is ergodic, with the further property that 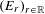 $(E_{r})_{r\in \mathbb{R}}$ is an increasing sequence of relations which are pairwise incomparable under
$(E_{r})_{r\in \mathbb{R}}$ is an increasing sequence of relations which are pairwise incomparable under  $\unicode[STIX]{x1D707}$-reducibility. In particular, we show that if
$\unicode[STIX]{x1D707}$-reducibility. In particular, we show that if 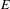 $E$ satisfies a natural separability condition, then this is the case as long as there exists a free Borel action of a countable non-abelian free group on
$E$ satisfies a natural separability condition, then this is the case as long as there exists a free Borel action of a countable non-abelian free group on 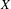 $X$, generating a subequivalence relation of
$X$, generating a subequivalence relation of 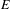 $E$ with respect to which
$E$ with respect to which  $\unicode[STIX]{x1D707}$ is ergodic.
$\unicode[STIX]{x1D707}$ is ergodic.