Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-08T14:30:59.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Horocycle flow orbits and lattice surface characterizations

Published online by Cambridge University Press:  28 September 2017

JON CHAIKA  and
KATHRYN LINDSEY
JON CHAIKA
Affiliation:
Department of Mathematics, University of Utah, Salt Lake City, UT 84112, USA email [email protected]
KATHRYN LINDSEY
Affiliation:
Department of Mathematics, University of Chicago, Chicago, IL 60637, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The orbit closure of any translation surface under the horocycle flow in almost any direction equals its 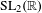$\text{SL}_{2}(\mathbb{R})$ orbit closure. This result gives rise to new characterizations of lattice surfaces in terms of the horocycle flow.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 6 , June 2019 , pp. 1441 - 1461
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Clavier, L.. Non-affine horocycle orbit closures on strata of translation surfaces: new examples. PhD Thesis, Department of Mathematics, Cornell University, 2016.Google Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory with a View Towards Number Theory (Graduate Texts in Mathematics, 259) . Springer, London, 2011.Google Scholar
Eskin, A., Mirzakhani, M. and Mohammadi, A.. Isolation, equidistribution, and orbit closures for the SL(2, ℝ) action on moduli space. Ann. of Math. (2) 182(2) (2015), 673–721.Google Scholar
Hooper, W. P. and Weiss, B.. The rel leaf and real-rel ray of the Arnoux–Yoccoz surface in genus 3. Preprint, 2015, arXiv:1506.06773.Google Scholar
Kontsevich, M. and Zorich, A.. Connected components of the moduli spaces of Abelian differentials with prescribed singularities. Invent. Math. 153(3) (2003), 631–678.Google Scholar
Lanneau, E., Nguyen, D.-M. and Wright, A.. Finiteness of Teichmüller curves in non-arithmetic rank 1 orbit closures. Preprint, 2015, arXiv:1504.03742.Google Scholar
Masur, H.. Interval exchange transformations and measured foliations. Ann. of Math. (2) 115(1) (1982), 169–200.Google Scholar
Smillie, J. and Weiss, B.. Examples of horocycle-invariant measures on the moduli space of translation surfaces. In preparation.Google Scholar
Smillie, J. and Weiss, B.. Minimal sets for flows on moduli space. Israel J. Math. 142 (2004), 249–260.Google Scholar
Smillie, J. and Weiss, B.. Veech’s dichotomy and the lattice property. Ergod. Th. & Dynam. Sys. 28(6) (2008), 1959–1972.Google Scholar
Smillie, J. and Weiss, B.. Characterizations of lattice surfaces. Invent. Math. 180(3) (2010), 535–557.Google Scholar
Smillie, J. and Weiss, B.. Examples of horocyle invariant measures on the moduli space of translation surfaces, I and II. Tech. Report 15, Mathematisches Forschungsinstitut Oberwolfach, March 2014.Google Scholar
Veech, W. A.. The Teichmüller geodesic flow. Ann. of Math. (2) 124(3) (1986), 441–530.Google Scholar
Wright, A.. Cylinder deformations in orbit closures of translation surfaces. Geom. Topol. 19(1) (2015), 413–438.Google Scholar