Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T10:35:38.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Homomorphisms between diffeomorphism groups

Published online by Cambridge University Press:  04 July 2013

KATHRYN MANN
KATHRYN MANN*
Affiliation:
Department of Mathematics, University of Chicago, 5734 University Avenue, Chicago, IL 60637, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For 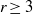$r\geq 3$, 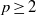$p\geq 2$, we classify all actions of the groups 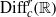${ \mathrm{Diff} }_{c}^{r} ( \mathbb{R} )$ and 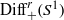${ \mathrm{Diff} }_{+ }^{r} ({S}^{1} )$ by 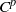${C}^{p} $-diffeomorphisms on the line and on the circle. This is the same as describing all non-trivial group homomorphisms between groups of compactly supported diffeomorphisms on 1-manifolds. We show that all such actions have an elementary form, which we call topologically diagonal. As an application, we answer a question of Ghys in the 1-manifold case: if 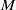$M$ is any closed manifold, and 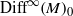${\mathrm{Diff} }^{\infty } \hspace{-2.0pt} \mathop{(M)}\nolimits_{0} $ injects into the diffeomorphism group of a 1-manifold, must 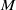$M$ be one-dimensional? We show that the answer is yes, even under more general conditions. Several lemmas on subgroups of diffeomorphism groups are of independent interest, including results on commuting subgroups and flows.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 1 , February 2015 , pp. 192 - 214
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banyaga, A.. On isomorphic classical diffeomorphism groups I. Proc. Amer. Math. Soc. 98 (1986), 113–118.Google Scholar
Banyaga, A.. The Structure of Classical Diffeomorphism Groups (Mathematics and Its Applications). Kluwer Academic Publishers, Dordrecht, 1997.CrossRefGoogle Scholar
Farb, B. and Franks, J.. Groups of homeomorphisms of one-manifolds, I: Actions of nonlinear groups. Preprint, 2001, arXiv:math/0107085v2.Google Scholar
Farb, B. and Franks, J.. Group actions on 1-manifolds, II: Extensions of Hölder’s theorem. Trans. Amer. Math. Soc. 355 (11) (2003), 4385–4396.Google Scholar
Filipkiewicz, R.. Isomorphisms between diffeomorphism groups. Ergod. Th. & Dynam. Sys. 2 (1982), 159–171.Google Scholar
Ghys, E.. Prolongements des difféomorphismes de la sphère. L’Enseign. Math. 37 (1991), 45–59.Google Scholar
Hölder, O.. Die Axiome der Quantität und die Lehre vom Mass. Ber. Verh. Sachs. Ges. Wiss. Leipzig, Math. Phys. C1 53 (1901), 1–64.Google Scholar
Kopell, N.. Commuting diffeomorphisms. Global Analysis (Proceedings of Symposia in Pure Mathematics, XIV). Eds. Chern, S.-S. and Smale, S.. Providence, RI, 1968, pp. 165–184.Google Scholar
Mather, J.. Commutators of diffeomorphisms. Comment. Math. Helv. 49 (1974), 512–528.Google Scholar
Mather, J.. Commutators of diffeomorphisms: II. Comment. Math. Helv. 50 (1975), 33–40.Google Scholar
Mather, J.. Commutators of diffeomorphisms, III: A group which is not perfect. Comment. Math. Helv. 60 (1985), 122–124.Google Scholar
Militon, E.. Continuous actions of the group of homeomorphisms of the circle on surfaces. Preprint, 2012, arXiv:1211.0846v2.Google Scholar
Militon, E.. Actions of groups of homeomorphisms on one-manifolds. Preprint, 2013, arXiv:1302.3737.Google Scholar
Navas, A.. Groups of Circle Diffeomorphisms. University of Chicago Press, Chicago, 2011.Google Scholar
Rybicki, T.. Isomorphisms between groups of diffeomorphisms. Proc. Amer. Math. Soc. 123 (1) (1995), 303–310.Google Scholar
Schweitzer, P.. Normal subgroups of diffeomorphism and homeomorphism groups of ${ \mathbb{R} }^{n} $ and other open manifolds. Preprint, 2012, arXiv:0911.4835v3.Google Scholar
Takens, F.. Characterization of a differentiable structure by its group of diffeomorphisms. Bol. Soc. Brasil. Mat. 10 (1979), 17–25.Google Scholar