Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:37:49.124Z Has data issue: false hasContentIssue false
  • English
  • Français

Homoclinic points, atoral polynomials, and periodic points of algebraic $\mathbb {Z}^d$-actions

Published online by Cambridge University Press:  16 May 2012

DOUGLAS LIND ,
KLAUS SCHMIDT  and
EVGENY VERBITSKIY
DOUGLAS LIND
Affiliation:
Department of Mathematics, University of Washington, Seattle, WA 98195, USA (email: [email protected])
KLAUS SCHMIDT
Affiliation:
Mathematics Institute, University of Vienna, Nordbergstrasse 15, A-1090 Vienna, Austria (email: [email protected])
EVGENY VERBITSKIY
Affiliation:
Mathematical Institute, University of Leiden, PO Box 9512, 2300 RA Leiden, The Netherlands Johann Bernoulli Institute for Mathematics and Computer Science, University of Groningen, PO Box 407, 9700 AK Groningen, The Netherlands (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

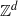Cyclic algebraic 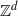${\mathbb {Z}^{d}}$-actions are defined by ideals of Laurent polynomials in 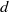$d$ commuting variables. Such an action is expansive precisely when the complex variety of the ideal is disjoint from the multiplicative 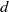$d$-torus. For such expansive actions it is known that the limit of the growth rate of periodic points exists and is equal to the entropy of the action. In an earlier paper the authors extended this result to ideals whose variety intersects the $d$-torus in a finite set. Here we further extend it to the case where the dimension of intersection of the variety with the 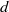$d$-torus is at most 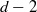$d-2$. The main tool is the construction of homoclinic points which decay rapidly enough to be summable.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 4 , August 2013 , pp. 1060 - 1081
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Agler, J., McCarthy, J. E. and Stankus, M.. Toral algebraic sets and function theory on polydisks. J. Geom. Anal. 16(4) (2006), 551–562.Google Scholar
[2]Aliev, I. and Smyth, C.. Solving algebraic equations in roots of unity. Preprint, 2010, Forum Math.,doi:10.1515/form.2011.087.Google Scholar
[3]Basu, S., Pollack, R. and Roy, M.-F.. Algorithms in Real Algebraic Geometry, 2nd edn. Springer, New York, 2009.Google Scholar
[4]Boyd, D.. Kronecker’s theorem and Lehmer’s problem for polynomials in several variables. J. Number Theory 13 (1981), 116–121.Google Scholar
[5]Deninger, C.. Fuglede-Kadison determinants and entropy for actions of discrete amenable groups. J. Amer. Math. Soc. 19 (2006), 737–758.Google Scholar
[6]Deninger, C. and Schmidt, K.. Expansive algebraic actions of discrete residually finite amenable groups and their entropy. Ergod. Th. & Dynam. Sys. 27 (2007), 769–786.Google Scholar
[7]den Dries, L. van. Tame Topology and O-minimal Structures. Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
[8]Edwards, H. M.. Divisor Theory. Birkhäuser, Boston, 1990.Google Scholar
[9]Gelfond, A. O.. Transcendental and Algebraic Numbers. Dover, New York, 1960.Google Scholar
[10]Granville, A. and Rudnick, Z.. Torsion points on curves. NATO Sci. Ser. II Math. Phys. Chem. 237 (2007), 85–92.Google Scholar
[11]Lind, D.. Dynamical properties of quasihyperbolic toral automorphisms. Ergod. Th. & Dynam. Sys. 2 (1982), 49–68.Google Scholar
[12]Lind, D. and Schmidt, K.. Homoclinic points of algebraic $\mathbf {Z}^d$-actions. J. Amer. Math. Soc. 12 (1999), 953–980.Google Scholar
[13]Lind, D., Schmidt, K. and Verbitskiy, E.. Entropy and growth rate of periodic points of algebraic $\mathbf {Z}^d$-actions. Dynamical Numbers: Interplay between Dynamical Systems and Number Theory (Contemporary Mathematics, 532). Eds. Kolyada, S., Manin, Yu., Möller, M., Moree, P. and Ward, T.. American Mathematical Society, Providence, RI, 2010.Google Scholar
[14]Lind, D., Schmidt, K. and Ward, T.. Mahler measure and entropy for commuting automorphisms of compact groups. Invent. Math. 101 (1990), 593–629.Google Scholar
[15]Mann, H. B.. On linear relations between roots of unity. Mathematika 12 (1965), 107–117.Google Scholar
[16]Schick, T.. $L^2$-determinant class and approximation of $L^2$-Betti numbers. Trans. Amer. Math. Soc. 353 (2001), 3247–3265.Google Scholar
[17]Schmidt, K.. Automorphisms of compact abelian groups and affine varieties. Proc. Lond. Math. Soc. 61 (1990), 480–496.Google Scholar
[18]Schmidt, K.. Dynamical Systems of Algebraic Origin. Birkhäuser, Basel, 1995.Google Scholar
[19]Schmidt, K. and Verbitskiy, E.. Abelian sandpiles and the harmonic model. Comm. Math. Phys. 292 (2009), 721–759.CrossRefGoogle Scholar
[20]Smyth, C. J.. An explicit formula for the Mahler measure of a family of 3-variable polynomials. J. Théor. Nombres Bordeaux 14 (2002), 683–700.Google Scholar
[21]Stein, E.. Harmonic Analysis: Real Variable Methods, Orthogonality, and Oscillatory Integrals. Princeton University Press, Princeton, 1993.Google Scholar