Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T04:11:44.191Z Has data issue: false hasContentIssue false
  • English
  • Français

Hölder shadowing on finite intervals

Published online by Cambridge University Press:  30 June 2014

SERGEY TIKHOMIROV
SERGEY TIKHOMIROV*
Affiliation:
Chebyshev Laboratory, Saint-Petersburg State University, 14th Line 29B, Vasilyevsky Island, St. Petersburg 199178, Russia Max Planck Institute for Mathematics in the Science, Inselstrasse 22, 04103 Leipzig, Germany email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For any 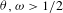${\it\theta},{\it\omega}>1/2$, we prove that, if any 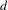$d$-pseudotrajectory of length 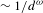${\sim}1/d^{{\it\omega}}$ of a diffeomorphism 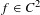$f\in C^{2}$ can be 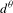$d^{{\it\theta}}$-shadowed by an exact trajectory, then 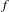$f$ is structurally stable. Previously it was conjectured [S. M. Hammel et al. Do numerical orbits of chaotic dynamical processes represent true orbits. J. Complexity3 (1987), 136–145; S. M. Hammel et al. Numerical orbits of chaotic processes represent true orbits. Bull. Amer. Math. Soc.19 (1988), 465–469] that for 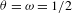${\it\theta}={\it\omega}=1/2$, this property holds for a wide class of non-uniformly hyperbolic diffeomorphisms. In the proof, we introduce the notion of a sublinear growth property for inhomogeneous linear equations and prove that it implies exponential dichotomy.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 6 , September 2015 , pp. 2000 - 2016
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anosov, D. V.. On a class of invariant sets of smooth dynamical systems. Proc. 5th Int. Conf. on Nonlinear Oscillators (Kiev, 1970). Vol. 2. Mathematical Institute of the Ukranian Academy of Science, Kiev, 1970, pp. 39–45.Google Scholar
Barreira, L. and Valls, C.. Stable manifolds for nonautonomous equations without exponential dichotomy. J. Differential Equations 221 (2006), 58–90.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer, Berlin, 1975.CrossRefGoogle Scholar
Chicone, C. and Latushkin, Yu. Evolution Semigroups in Dynamical Systems and Differential Equations (Mathematical Surveys and Monographs, 70). American Mathematical Society, Providence, RI, 1999.CrossRefGoogle Scholar
Coffman, C. V. and Schaeffer, J. J.. Dichotomies for linear difference equations. Math. Ann. 172 (1967), 139–166.CrossRefGoogle Scholar
Coppel, W. A.. Dichotomies in stability theory (Lecture Notes in Mathematics, 629). Springer, Berlin, 1978.CrossRefGoogle Scholar
Fisher, T.. PhD Thesis, Penn State University, 2006.Google Scholar
Gogolev, A.. Diffeomorphisms Hölder conjugate to Anosov diffeomorphisms. Ergod. Th. & Dynam. Sys. 30 (2010), 441–456.CrossRefGoogle Scholar
Hammel, S. M., Yorke, J. A. and Grebogi, C.. Do numerical orbits of chaotic dynamical processes represent true orbits. J. Complexity 3 (1987), 136–145.CrossRefGoogle Scholar
Hammel, S. M., Yorke, J. A. and Grebogi, C.. Numerical orbits of chaotic processes represent true orbits. Bull. Amer. Math. Soc. 19 (1988), 465–469.CrossRefGoogle Scholar
Huy, N. T. and Van Minh, N.. Exponential dichotomy of difference equations and applications to evolution equations on the half-line. Comput. Math. Appl. 42 (2001), 301–311.CrossRefGoogle Scholar
Koropecki, A. and Pujals, E.. Some consequences of the shadowing property in low dimensions. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2012.195, published online 8 March 2013.Google Scholar
Maizel, A. D.. On stability of solutions of systems of differential equations. Ural. Politehn. Inst. Trudy 51 (1954), 20–50.Google Scholar
Mañé, R.. Characterizations of AS diffeomorphisms. Geometry and Topology (Lecture Notes in Mathematics, 597). Springer, Berlin, 1977, pp. 389–394.CrossRefGoogle Scholar
Morimoto, A.. The method of pseudo-orbit tracing and stability of dynamical systems. Seminar Note. Vol. 39. Tokyo University, Tokyo, 1979.Google Scholar
Osipov, A. V., Pilyugin, S. Yu and Tikhomirov, S. B.. Periodic shadowing and Ω-stability. Regul. Chaotic Dyn. 15 (2010), 404–417.CrossRefGoogle Scholar
Palmer, K.. Shadowing in Dynamical Systems. Theory and Applications. Kluwer, Dordrecht, 2000.CrossRefGoogle Scholar
Palmer, K. J.. Exponential dichotomies and transversal homoclinic points. J. Differential Equations 55 (1984), 225–256.CrossRefGoogle Scholar
Palmer, K. J.. Exponential dichotomies and Fredholm operators. Proc. Amer. Math. Soc. 104 (1988), 149–156.CrossRefGoogle Scholar
Palmer, K. J.. Exponential dichotomies, the shadowing lemma and transversal homoclinic points. Dynam. Rep. 1 (1988), 265–306.CrossRefGoogle Scholar
Yu Pilyugin, S.. Shadowing in Dynamical Systems (Lecture Notes in Mathematics, 1706). Springer, Berlin, 1999.Google Scholar
Yu Pilyugin, S.. Generalizations of the notion of hyperbolicity. J. Difference Equ. Appl. 12 (2006), 271–282.CrossRefGoogle Scholar
Pilyugin, S. Yu. Variational shadowing. Discrete Contin. Dyn. Syst. Ser. B 14 (2010), 733–737.Google Scholar
Pilyugin, S. Yu and Tikhomirov, S. B.. Lipschitz Shadowing implies structural stability. Nonlinearity 23 (2010), 2509–2515.CrossRefGoogle Scholar
Yu Pilyugin, S.. Theory of pseudo-orbit shadowing in dynamical systems. Differ. Equ. 47 (2011), 1929–1938.CrossRefGoogle Scholar
Pliss, V. A.. Bounded solutions of nonhomogeneous linear systems of differential equations. Problems in the Asymptotic Theory of Nonlinear Oscillations. Naukova Dumbka, Kiev, 1977, pp. 168–173.Google Scholar
Robinson, C.. Stability theorems and hyperbolicity in dynamical systems. Rocky Mountain J. Math. 7 (1977), 425–437.CrossRefGoogle Scholar
Sawada, K.. Extended f-orbits are approximated by orbits. Nagoya Math. J. 79 (1980), 33–45.CrossRefGoogle Scholar
Slyusarchuk, V.. Exponential dichotomy of solutions of discrete systems. Ukrain. Mat. Zh. 35 (1983), 109–115.CrossRefGoogle Scholar
Todorov, D.. Generalizations of analogs of theorems of Maizel and Pliss and their application in Shadowing Theory. Discrete Contin. Dyn. Syst. Ser. A 33 (2013), 4187–4205.CrossRefGoogle Scholar