Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-16T15:31:15.547Z Has data issue: false hasContentIssue false
  • English
  • Français

Helicity of vector fields preserving a regular contact form and topologically conjugate smooth dynamical systems

Published online by Cambridge University Press:  29 June 2012

STEFAN MÜLLER  and
PETER SPAETH
STEFAN MÜLLER
Affiliation:
Korea Institute for Advanced Study, Seoul, Korea (email: [email protected], [email protected])
PETER SPAETH
Affiliation:
Korea Institute for Advanced Study, Seoul, Korea (email: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We compute the helicity of a vector field preserving a regular contact form on a closed three-dimensional manifold, and improve results of Gambaudo and Ghys [Enlacements asymptotiques. Topology 36(6) (1997), 1355–1379] relating the helicity of the suspension of a surface isotopy to the Calabi invariant of the isotopy. Based on these results, we provide positive answers to two questions posed by Arnold in [The asymptotic Hopf invariant and its applications. Selecta Math. Soviet. 5(4) (1986), 327–345]. In the presence of a regular contact form that is also preserved, the helicity extends to an invariant of an isotopy of volume-preserving homeomorphisms, and is invariant under conjugation by volume-preserving homeomorphisms. A similar statement also holds for suspensions of surface isotopies and surface diffeomorphisms. This requires the techniques of topological Hamiltonian and contact dynamics developed by Banyaga and Spaeth [On the uniqueness of generating Hamiltonians for topological strictly contact isotopies. Preprint, 2012], Buhovsky and Seyfaddini [Uniqueness of generating Hamiltonians for continuous Hamiltonian flows. J. Symplectic Geom. to appear, arXiv:1003.2612v2], Müller [The group of Hamiltonian homeomorphisms in the 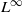$L^\infty $-norm. J. Korean Math. Soc.45(6) (2008), 1769–1784], Müller and Oh [The group of Hamiltonian homeomorphisms and 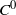$C^0$-symplectic topology. J. Symplectic Geom. 5(2) (2007), 167–219], Müller and Spaeth [Topological contact dynamics I: symplectization and applications of the energy-capacity inequality. Preprint, 2011, arXiv:1110.6705v2] and Viterbo [On the uniqueness of generating Hamiltonian for continuous limits of Hamiltonians flows. Int. Math. Res. Not. (2006), 34028; Erratum, Int. Math. Res. Not. (2006), 38748]. Moreover, we generalize an example of Furstenberg [Strict ergodicity and transformation of the torus. Amer. J. Math. 83 (1961), 573–601] on topologically conjugate but not 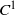$C^1$-conjugate area-preserving diffeomorphisms of the two-torus to trivial 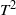$T^2$-bundles, and construct examples of Hamiltonian and contact vector fields that are topologically conjugate but not $C^1$-conjugate. Higher-dimensional helicities are considered briefly at the end of the paper.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 5 , October 2013 , pp. 1550 - 1583
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[AK98]Arnold, V. I. and Khesin, B. A.. Topological Methods in Hydrodynamics (Applied Mathematical Sciences, 125). Springer, New York, 1998.Google Scholar
[Arn86]Arnol’d, V. I.. The asymptotic Hopf invariant and its applications. Selecta Math. Soviet. 5(4) (1986), 327–345, selected translations.Google Scholar
[Ban78a]Banyaga, A.. The group of diffeomorphisms preserving a regular contact form. Topology and Algebra (Proc. Colloq., Eidgenöss. Tech. Hochsch., Zurich, 1977) (Monographies de L’Enseignement Mathématique, 26). Université de Genève, Geneva, 1978, pp. 47–53.Google Scholar
[Ban78b]Banyaga, A.. Sur la structure du groupe des difféomorphismes qui préservent une forme symplectique. Comment. Math. Helv. 53(2) (1978), 174–227.CrossRefGoogle Scholar
[Ban97]Banyaga, A.. The Structure of Classical Diffeomorphism Groups (Mathematics and its Applications, 400). Kluwer, Dordrecht, 1997.Google Scholar
[Bla10]Blair, D. E.. Riemannian Geometry of Contact and Symplectic Manifolds, 2nd edn(Progress in Mathematics, 203). Birkhäuser, Boston, MA, 2010.CrossRefGoogle Scholar
[BS11]Buhovsky, L. and Seyfaddini, S.. Uniqueness of generating Hamiltonians for continuous Hamiltonian flows. J. Symplectic Geom. to appear, arXiv:1003.2612v2.Google Scholar
[BS12]Banyaga, A. and Spaeth, P.. On the uniqueness of generating Hamiltonians for topological strictly contact isotopies. Preprint, 2012, http://newton.kias.re.kr/∼spaeth.Google Scholar
[BW58]Boothby, W. M. and Wang, H. C.. On contact manifolds. Ann. of Math. (2) 68 (1958), 721–734.CrossRefGoogle Scholar
[EE69]Earle, C. J. and Eells, J.. A fibre bundle description of Teichmüller theory. J. Differential Geom. 3 (1969), 19–43.CrossRefGoogle Scholar
[EG00]Etnyre, J. and Ghrist, R.. Contact topology and hydrodynamics. I. Beltrami fields and the Seifert conjecture. Nonlinearity 13(2) (2000), 441–458.Google Scholar
[Fat80]Fathi, A.. Structure of the group of homeomorphisms preserving a good measure on a compact manifold. Ann. Sci. Éc. Norm. Supér. (4) 13(1) (1980), 45–93.Google Scholar
[Fur61]Furstenberg, H.. Strict ergodicity and transformation of the torus. Amer. J. Math. 83 (1961), 573–601.Google Scholar
[Gei08]Geiges, H.. An introduction to Contact Topology (Cambridge Studies in Advanced Mathematics, 109). Cambridge University Press, Cambridge, 2008.CrossRefGoogle Scholar
[GG97]Gambaudo, J.-M. and Ghys, É.. Enlacements asymptotiques. Topology 36(6) (1997), 1355–1379.CrossRefGoogle Scholar
[GG01]Gambaudo, J.-M. and Ghys, É.. Signature asymptotique d’un champ de vecteurs en dimension 3. Duke Math. J. 106(1) (2001), 41–79.CrossRefGoogle Scholar
[GH55]Gottschalk, W. H. and Hedlund, G. A.. Topological Dynamics (American Mathematical Society Colloquium Publications, 36). American Mathematical Society, Providence, RI, 1955.Google Scholar
[Ghy07]Ghys, É.. Knots and dynamics. Proceedings of the International Congress of Mathematicians (Madrid, Spain, 2006), I. European Mathematical Society, Zürich, 2007, pp. 247–277.Google Scholar
[Hir63]Hirsch, M. W.. Obstruction theories for smoothing manifolds and maps. Bull. Amer. Math. Soc. 69 (1963), 352–356.Google Scholar
[KH95]Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54). Cambridge University Press, Cambridge, 1995.Google Scholar
[Khe03]Khesin, B. A.. Geometry of higher helicities. Mosc. Math. J. 3(3) (2003), 989–1011, dedicated to Vladimir Igorevich Arnold on the occasion of his 65th birthday.CrossRefGoogle Scholar
[Kod95a]Kodaka, K.. Anzai and Furstenberg transformations on the $2$-torus and topologically quasi-discrete spectrum. Canad. Math. Bull. 38(1) (1995), 87–92.Google Scholar
[Kod95b]Kodaka, K.. Tracial states on crossed products associated with Furstenberg transformations on the 2-torus. Studia Math. 115(2) (1995), 183–187.Google Scholar
[KV03]Kotschick, D. and Vogel, T.. Linking numbers of measured foliations. Ergod. Th. & Dynam. Sys. 23(2) (2003), 541–558.CrossRefGoogle Scholar
[Mar71]Martinet, J.. Formes de contact sur les variétés de dimension 3. Singularities – Symposium, II (Liverpool, UK 1969/1970) (Lecture Notes in Mathematics, 209). Springer, Berlin, 1971, pp. 142–163.Google Scholar
[MO07]Müller, S. and Oh, Y.-G.. The group of Hamiltonian homeomorphisms and $C^0$-symplectic topology. J. Symplectic Geom. 5(2) (2007), 167–219.Google Scholar
[MS98]McDuff, D. and Salamon, D.. Introduction to Symplectic Topology, 2nd edn(Oxford Mathematical Monographs). Oxford University Press, New York, 1998.Google Scholar
[MS11]Müller, S. and Spaeth, P.. Topological contact dynamics I: symplectization and applications of the energy-capacity inequality. Preprint, 2011, arXiv:1110.6705v2.Google Scholar
[M{ü}l08a]Müller, S.. The group of Hamiltonian homeomorphisms and topological symplectic topology. PhD Thesis, Department of Mathematics, University of Wisconsin – Madison, 2008.Google Scholar
[M{ü}l08b]Müller, S.. The group of Hamiltonian homeomorphisms in the $L^\infty $-norm. J. Korean Math. Soc. 45(6) (2008), 1769–1784.Google Scholar
[M{ü}l11]Müller, S.. A note on the volume flux of smooth and continuous strictly contact isotopies. Preprint, 2011, arXiv:1107.4869v1.Google Scholar
[Mun59]Munkres, J.. Obstructions to the smoothing of piecewise-differentiable homeomorphisms. Bull. Amer. Math. Soc. 65 (1959), 332–334.Google Scholar
[Mun60]Munkres, J.. Obstructions to the smoothing of piecewise-differentiable homeomorphisms. Ann. of Math. (2) 72 (1960), 521–554.Google Scholar
[Mun65]Munkres, J. R.. Higher obstructions to smoothing. Topology 4 (1965), 27–45.Google Scholar
[Oh06]Oh, Y.-G.. $C^ 0$-coerciveness of Moser’s problem and smoothing area preserving homeomorphisms. Preprint, 2006, arXiv:math/0601183v5.Google Scholar
[Pol01]Polterovich, L.. The Geometry of the Group of Symplectic Diffeomorphisms (Lectures in Mathematics ETH Zürich). Birkhäuser, Basel, 2001.Google Scholar
[Riv02]Rivière, T.. High-dimensional helicities and rigidity of linked foliations. Asian J. Math. 6(3) (2002), 505–533.Google Scholar
[Rou90]Rouhani, H.. A Furstenberg transformation of the $2$-torus without quasi-discrete spectrum. Canad. Math. Bull. 33(3) (1990), 316–322.CrossRefGoogle Scholar
[Sik07]Sikorav, J.-C.. Approximation of a volume-preserving homeomorphism by a volume-preserving diffeomorphism. Preprint, 2007, http://www.umpa.ens-lyon.fr/∼symplexe/publications.php.Google Scholar
[Vit06]Viterbo, C.. On the uniqueness of generating Hamiltonian for continuous limits of Hamiltonians flows. Int. Math. Res. Not. (2006), Art. ID 34028; MR 2233715(2007h:37081a). Erratum. Int. Math. Res. Not. (2006), Art. ID 38748; MR 2272093 (2007h:37081b).Google Scholar