Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T01:13:53.956Z Has data issue: false hasContentIssue false
  • English
  • Français

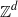group shifts and Bernoulli factors

Published online by Cambridge University Press:  01 April 2008

MIKE BOYLE  and
MICHAEL SCHRAUDNER
MIKE BOYLE
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742-4015, USA (email: [email protected]) Centro de Modelamiento Matemático, Universidad de Chile, Av. Blanco Encalada 2120, Piso 7, Santiago de Chile, Chile (email: [email protected])
MICHAEL SCHRAUDNER
Affiliation:
Centro de Modelamiento Matemático, Universidad de Chile, Av. Blanco Encalada 2120, Piso 7, Santiago de Chile, Chile (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, a group shift is an expansive action of 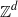on a compact metrizable zero-dimensional group by continuous automorphisms. All group shifts factor topologically onto equal-entropy Bernoulli shifts; abelian group shifts factor by continuous group homomorphisms onto canonical equal-entropy Bernoulli group shifts; and completely positive entropy abelian group shifts are weakly algebraically equivalent to these Bernoulli factors. A completely positive entropy group (even vector) shift need not be topologically conjugate to a Bernoulli shift, and the Pinsker factor of a vector shift need not split topologically.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 2: William Parry Memorial Volume , April 2008 , pp. 367 - 387
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Boyle, M.. Factoring factor maps. J. London Math. Soc. (2) 57(2) (1998), 491–502.CrossRefGoogle Scholar
[2]Boyle, M., Lind, D. and Rudolph, D.. The automorphism group of a shift of finite type. Trans. Amer. Math. Soc. 306(1) (1988), 71–114.CrossRefGoogle Scholar
[3]Boyle, M. and Schraudner, M.. shifts of finite type without equal-entropy Bernoulli factors. J. Difference Equ. Appl. Special issue on Combinatorial and Topological Dynamics to appear.Google Scholar
[4]Einsiedler, M. and Schmidt, K.. The adjoint action of an expansive algebraic action. Monatsh. Math. 135(3) (2002), 203–220.CrossRefGoogle Scholar
[5]Fagnani, F.. Some results on the classification of expansive automorphisms of compact abelian groups. Ergod. Th. & Dynam. Sys. 16(1) (1996), 45–50.CrossRefGoogle Scholar
[6]Fagnani, F.. Shifts on compact and discrete Lie groups: algebraic-topological invariants and classification problems. Adv. Math. 127(2) (1997), 283–306.CrossRefGoogle Scholar
[7]Hochman, M. and Meyerovitch, T.. A characterization of the entropies of multidimensional shifts of finite type. Mathematics (2007). ArXiv DS/0703206.Google Scholar
[8]Johnson, A., Kass, S. and Madden, K.. Projectional entropy in higher dimensional shifts of finite type. Complex Systems to appear.Google Scholar
[9]Kitchens, B.. Expansive dynamics on zero-dimensional groups. Ergod. Th. & Dynam. Sys. 7 (1987), 249–261.CrossRefGoogle Scholar
[10]Kitchens, B.. Multidimensional convolutional codes. SIAM J. Discrete Math. 15(3) (2002), 367–381.CrossRefGoogle Scholar
[11]Kitchens, B.. The structure of d-dimensional vector shifts and convolutional codes, 2003, 18 pp., unpublished manuscript.Google Scholar
[12]Kitchens, B. and Schmidt, K.. Automorphisms of compact groups. Ergod. Th. & Dynam. Sys. 9 (1989), 691–735.CrossRefGoogle Scholar
[13]Lind, D. and Schmidt, K.. Homoclinic points of algebraic -actions. J. Amer. Math. Soc. 12(4) (1999), 953–980.CrossRefGoogle Scholar
[14]Lind, D., Schmidt, K. and Ward, T.. Mahler measure and entropy for commuting automorphisms of compact groups. Invent. Math. 101 (1990), 593–629.CrossRefGoogle Scholar
[15]Ornstein, D. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48 (1987), 1–141.CrossRefGoogle Scholar
[16]Parry, W.. Intrinsic Markov chains. Trans. Amer. Math. Soc. 112 (1964), 55–66.CrossRefGoogle Scholar
[17]Rudolph, D. J. and Schmidt, K.. Almost block independence and Bernoullicity of -actions by automorphisms of compact abelian groups. Invent. Math. 120(3) (1995), 455–488.CrossRefGoogle Scholar
[18]Rudolph, D. and Weiss, B.. Entropy and mixing for amenable group actions. Ann. Math. (2) 151(3) (2000), 1119–1150.CrossRefGoogle Scholar
[19]Schmidt, K.. Dynamical Systems of Algebraic Origin. Birkhäuser, Basel, 1995.Google Scholar