Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T18:07:23.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Group actions on Smale space 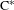$\text{C}^{\ast }$-algebras

Part of: Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  10 April 2019

ROBIN J. DEELEY  and
KAREN R. STRUNG
ROBIN J. DEELEY
Affiliation:
Department of Mathematics, University of Colorado Boulder Campus Box 395, Boulder, CO80309-0395, USA email [email protected]
KAREN R. STRUNG
Affiliation:
Institute for Mathematics, Astrophysics, and Particle Physics, Radboud University, Postbus 9010, 6500 GLNijmegen, The Netherlands email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Group actions on a Smale space and the actions induced on the 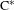$\text{C}^{\ast }$-algebras associated to such a dynamical system are studied. We show that an effective action of a discrete group on a mixing Smale space produces a strongly outer action on the homoclinic algebra. We then show that for irreducible Smale spaces, the property of finite Rokhlin dimension passes from the induced action on the homoclinic algebra to the induced actions on the stable and unstable 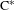$\text{C}^{\ast }$-algebras. In each of these cases, we discuss the preservation of properties (such as finite nuclear dimension, 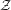${\mathcal{Z}}$-stability, and classification by Elliott invariants) in the resulting crossed products.

Keywords

Smale spacesclassification of nuclear C∗ -algebrasgroup actionsRokhlin property

MSC classification

Primary: 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 9 , September 2020 , pp. 2368 - 2398
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. L., Kitchens, B. and Marcus, B. H.. Finite group actions on shifts of finite type. Ergod. Th. & Dynam. Sys. 5 (1985), 1–25.10.1017/S0143385700002728Google Scholar
Anderson, J. E. and Putnam, I. F.. Topological invariants for substitution tilings and their associated C*-algebras. Ergod. Th. & Dynam. Sys. 18(3) (1998), 509–537.10.1017/S0143385798100457Google Scholar
Archey, D.. Crossed product C ∗ -algebras by finite group actions with the tracial Rokhlin property. Rocky Mountain J. Math. 41(6) (2011), 1755–1768.10.1216/RMJ-2011-41-6-1755Google Scholar
Baake, M. and Roberts, J. A. G.. Symmetries and reversing symmetries of toral automorphisms. Nonlinearity 14 (2001), R1–R24.Google Scholar
Bosa, J., Brown, N. P., Sato, Y., Tikuisis, A., White, S. and Winter, W.. Covering dimension of C ∗ -algebras and 2-coloured classification. Mem. Amer. Math. Soc. 257(1233) (2019). doi:10.1090/memo/1233.Google Scholar
Boyle, M.. Open problems in symbolic dynamics. Geometric and Probabilistic Structures in Dynamics (Contemporary Mathematics, 469). American Mathematical Society, Providence, RI, 2008, pp. 69–118.10.1090/conm/469/09161Google Scholar
Boyle, M., Lind, D. and Rudolph, D.. The automorphism group of a shift of finite type. Trans. Amer. Math. Soc. 306(1) (1988), 71–114.10.1090/S0002-9947-1988-0927684-2Google Scholar
Brown, N. P., Tikuisis, A. and Zelenberg, A. M.. Rohklin dimension for C*-correspondences. Houston J. Math. 44(2) (2017), 613–643.Google Scholar
Connes, A.. Outer conjugacy classes of automorphisms of factors. Ann. Sci. Éc. Norm. Supér. (4) 8(3) (1975), 383–419.Google Scholar
Connes, A.. Periodic automorphisms of the hyperfinite factor of type II1. Acta Sci. Math. (Szeged) 39(1–2) (1977), 39–66.Google Scholar
Connes, A.. Noncommutative Geometry. Academic Press, San Diego, CA, 1994.Google Scholar
Deeley, R. J. and Strung, K. R.. Nuclear dimension and classification of C ∗ -algebras associated to Smale spaces. Trans. Amer. Math. Soc. 370(5) (2018), 3467–3485.10.1090/tran/7046Google Scholar
Dumitraşcu, C. D.. On an intermediate bivariant theory for C ∗ -algebras, I. J. Noncommut. Geom. 10(2) (2016), 1083–1130.10.4171/JNCG/255Google Scholar
Echterhoff, S., Lück, W., Phillips, N. C. and Walters, S.. The structure of crossed products of irrational rotation algebras by finite subgroups of SL2(ℤ). J. Reine Angew. Math. 639 (2010), 173–221.Google Scholar
Gardella, E.. Rokhlin dimension for compact group actions. Indiana Univ. Math. J 66 (2017), 659–703.Google Scholar
Giordano, T., Putnam, I. F. and Skau, C. F.. Topological orbit equivalence and C ∗ -crossed products. J. Reine Angew. Math. 469 (1995), 51–111.Google Scholar
Guentner, E., Higson, N. and Trout, J.. Equivariant E-theory for C*-algebras. Mem. Amer. Math. Soc. 148(703) (2000).Google Scholar
Handelman, D. and Rossmann, W.. Actions of compact groups on AF C ∗ -algebras. Illinois J. Math. 29(1) (1985), 51–95.Google Scholar
Herman, R. H. and Jones, V. F. R.. Period two automorphisms of UHF C ∗ -algebras. J. Funct. Anal. 45(2) (1982), 169–176.Google Scholar
Herman, R. H. and Ocneanu, A.. Stability for integer actions on UHF C ∗ -algebras. J. Funct. Anal. 59(1) (1984), 132–144.Google Scholar
Hirshberg, I. and Phillips, N. C.. Rokhlin dimension: obstructions and permanence properties. Doc. Math. 20 (2015), 199–236.Google Scholar
Hirshberg, I., Szabó, G., Wu, J. and Winter, W.. Rokhlin dimension for flows. Comm. Math. Phys. 353(1) (2017), 253–316.Google Scholar
Hirshberg, I., Winter, W. and Zacharias, J.. Rokhlin dimension and C ∗ -dynamics. Comm. Math. Phys. 335(2) (2015), 637–670.Google Scholar
Holton, C. G.. The Rohlin property for shifts of finite type. J. Funct. Anal. 229(2) (2005), 277–299.Google Scholar
Hou, C.. On the traces of the groupoid C ∗ -algebras from Smale spaces. Chin. Ann. Math. Ser. A (2) (2003).Google Scholar
Izumi, M.. Finite group actions on C ∗ -algebras with the Rohlin property. I. Duke Math. J. 122(2) (2004), 233–280.Google Scholar
Izumi, M.. Finite group actions on C ∗ -algebras with the Rohlin property. II. Adv. Math. 184(1) (2004), 119–160.Google Scholar
Jiang, X. and Su, H.. On a simple unital projectionless C ∗ -algebra. Amer. J. Math. 121(2) (1999), 359–413.Google Scholar
Kasparov, G. G.. Equivariant KK -theory and the Novikov conjecture. Invent. Math. 91 (1988), 147–201.Google Scholar
Kellendonk, J.. Noncommutative geometry of tilings and gap labelling. Rev. Math. Phys. 7(7) (1995), 1133–1180.Google Scholar
Killough, D. B.. Ring structures on the K-theory of C*-algebras associated to Smale spaces. PhD Thesis, University of Victoria, 2009.Google Scholar
Kishimoto, A.. The Rohlin property for automorphisms of UHF algebras. J. Reine Angew. Math. 465 (1995), 183–196.Google Scholar
Kishimoto, A.. The Rohlin property for shifts on UHF algebras and automorphisms of Cuntz algebras. J. Funct. Anal. 140(1) (1996), 100–123.Google Scholar
Kishimoto, A.. Automorphisms of AT algebras with the Rohlin property. J. Operator Theory 40(2) (1998), 277–294.Google Scholar
Liao, H.-C.. Rokhlin dimension of Z m actions on simple C*-algebras. Int. J. Math. 28 (2017), 22.10.1142/S0129167X17500501Google Scholar
Lin, H.. Tracially AF C ∗ -algebras. Trans. Amer. Math. Soc. 353 (2001), 693–722.Google Scholar
Lin, H.. Crossed products and minimal dynamical systems. J. Topol. Anal. 10(2) (2018), 447–469.Google Scholar
Lin, H. and Phillips, N. C.. Crossed products by minimal homeomorphisms. J. Reine Angew Math. 641 (2010), 95–122.Google Scholar
Lind, D. and Marcus, B. H.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1999.Google Scholar
Matsumoto, K.. On automorphisms of C ∗ -algebras associated with subshifts. J. Operator Theory 44 (2000), 81–112.Google Scholar
Matui, H. and Sato, Y.. 𝓩-stability of crossed products by strongly outer actions. Comm. Math. Phys. 314(1) (2012), 193–228.10.1007/s00220-011-1392-9Google Scholar
Matui, H. and Sato, Y.. Decomposition rank of UHF-absorbing C ∗ -algebras. Duke Math. J. 163(14) (2014), 2687–2708.Google Scholar
Nasu, M.. Textile systems for endomorphisms and automorphisms of the shift. Mem. Amer. Math. Soc. 114(546) (1995).Google Scholar
Osaka, H.. The tracial Rokhlin property for automorphisms of simple C ∗ -algebras and its applications. Mem. Inst. Sci. Engrg. Ritsumeikan Univ. (63) (2004), 41–47.Google Scholar
Pasnicu, C.. Homomorphisms of Bunce–Deddens algebras. Pacific J. Math. 155(1) (1992), 157–167.10.2140/pjm.1992.155.157Google Scholar
Pesin, Y. and Weiss, H.. A multifractal analysis of equilibrium measures for conformal expanding maps and Moran-like geometric constructions. J. Stat. Phys. 86(1–2) (1997), 233–275.10.1007/BF02180206Google Scholar
Phillips, N. C.. Freeness of actions of finite groups on C ∗ -algebras. Operator Structures and Dynamical Systems (Contemporary Mathematics, 503). American Mathematical Society, Providence, RI, 2009, pp. 217–257.10.1090/conm/503/09902Google Scholar
Phillips, N. C.. Finite cyclic group actions with the tracial Rokhlin property. Trans. Amer. Math. Soc. 367(8) (2015), 5271–5300.Google Scholar
Pollicott, M.. A note on the growth of periodic points for commuting toral automorphism. ISRN Geometry 2012 (2012), 15.10.5402/2012/165808Google Scholar
Putnam, I. F.. The C ∗ -algebras associated with minimal homeomorphisms of the Cantor set. Pacific J. Math. 136(2) (1989), 329–353.Google Scholar
Putnam, I. F.. C ∗ -algebras from Smale spaces. Canad. J. Math. 48(1) (1996), 175–195.Google Scholar
Putnam, I. F. and Spielberg, J. S.. The structure of C ∗ -algebras associated with hyperbolic dynamical systems. J. Funct. Anal. 163(2) (1999), 279–299.Google Scholar
Renault, J.. A Groupoid Approach to C ∗ -Algebras. Springer, Berlin, 1980.Google Scholar
Rørdam, M.. The stable and the real rank of 𝓩-absorbing C ∗ -algebras. Internat. J. Math. 15(10) (2004), 1065–1084.Google Scholar
Ruelle, D.. Noncommutative algebras for hyperbolic diffeomorphisms. Invent. Math. 93(1) (1988), 1–13.Google Scholar
Ruelle, D.. Thermodynamic Formalism, 2nd edn. Cambridge University Press, Cambridge, 2004.Google Scholar
Ruelle, D. and Sullivan, D.. Currents, flows and diffeomorphisms. Topology 14(4) (1975), 319–327.Google Scholar
Sato, Y.. Actions of amenable groups and crossed products of ${\mathcal{Z}}$-absorbing $C^{\ast }$-algebras. Proc. 9th MSJ-SI, to appear, 2016.Google Scholar
Schechtman, D., Blech, I., Gratias, D. and Cahn, J. W.. Metallic phase with long range orientational order and no translational symmetry. Phys. Rev. Lett. (53) (1984), 1951–1953.Google Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. (N.S.) 73 (1967), 747–817.Google Scholar
Starling, C.. Finite symmetry group actions on substitution tiling C*-algebras. Münster J. Math. 7 (2014), 381–412.Google Scholar
Strung, K. R.. On the classification of C ∗ -algebras of minimal product systems of the Cantor set and an odd dimensional sphere. J. Funct. Anal. 268(3) (2015), 671–689.10.1016/j.jfa.2014.10.014Google Scholar
Szabó, G.. The Rokhlin dimension of topological Z m-actions. Proc. Lond. Math. Soc. (3) 110(3) (2015), 673–694.Google Scholar
Szabó, G., Wu, J. and Zacharias, J.. Rokhlin dimension for actions of residually finite groups. Preprint, 2015, arXiv:math.OA/1408.6096.Google Scholar
Tezer, C.. Automorphism groups of a class of expanding attractors. Nagoya Math. J. 134 (1994), 29–55.Google Scholar
Tikuisis, A.. Nuclear dimension, 𝓩-stability, and algebraic simplicity for stably projectionless C ∗ -algebras. Math. Ann. 358(3) (2014), 729–778.Google Scholar
Tikuisis, A., White, S. and Wilhelm, W.. Quasidiagonality of nuclear C∗ -algebras. Ann. of Math. (2) 185(1) (2017), 229–284.Google Scholar
Toms, A. S. and Winter, W.. Minimal dynamics and the classification of C ∗ -algebras. Proc. Natl. Acad. Sci. USA 106(40) (2009), 16942–16943.Google Scholar
Tu, J.-L.. La conjecture de Baum–Connes pour les feuilletages moyennables. K-Theory 17(3) (1999), 215–264.Google Scholar
Wieler, S.. Smale spaces via inverse limits. Ergod. Th. & Dynam. Sys. 34(06) (2014), 2066–2092.Google Scholar
Williams, R. F.. Expanding attractors. Publ. Math. Inst. Hautes Études Sci. 43 (1974), 169–203.Google Scholar
Winter, W.. Classifying crossed products. Amer. J. Math. 138(3) (2016), 793–820.Google Scholar
Winter, W. and Zacharias, J.. Completely positive maps of order zero. Münster J. Math. 2 (2009), 311–324.Google Scholar