Let 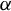$\alpha $ be a 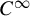$C^{\infty }$ volume-preserving action on a closed n-manifold M by a lattice 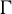$\Gamma $ in 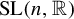$\mathrm {SL}(n,\mathbb {R})$, 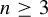$n\ge 3$. Assume that there is an element 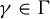$\gamma \in \Gamma $ such that 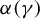$\alpha (\gamma )$ admits a dominated splitting. We prove that the manifold M is diffeomorphic to the torus 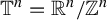${{\mathbb T}^{n}={\mathbb R}^{n}/{\mathbb Z}^{n}}$ and 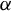$\alpha $ is smoothly conjugate to an affine action. Anosov diffeomorphisms and partial hyperbolic diffeomorphisms admit a dominated splitting. We obtained a topological global rigidity when 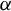$\alpha $ is 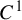$C^{1}$. We also prove similar theorems for actions on 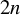$2n$-manifolds by lattices in $\textrm {Sp}(2n,{\mathbb R})$ with 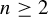$n\ge 2$ and 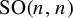$\mathrm {SO}(n,n)$ with 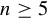$n\ge 5$.