Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T14:02:54.160Z Has data issue: false hasContentIssue false
  • English
  • Français

Gibbs measures for foliated bundles with negatively curved leaves

Published online by Cambridge University Press:  15 December 2016

SÉBASTIEN ALVAREZ
SÉBASTIEN ALVAREZ*
Affiliation:
IMPA, Est. D. Castorina 110, 22460-320, Rio de Janeiro, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we develop a notion of Gibbs measure for the geodesic flow tangent to a foliated bundle over a compact negatively curved base. We also develop a notion of $F$-harmonic measure and prove that there exists a natural bijective correspondence between these two concepts. For projective foliated bundles with 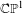$\mathbb{C}\mathbb{P}^{1}$-fibers without transverse invariant measure, we show the uniqueness of these measures for any Hölder potential on the base. In that case we also prove that $F$-harmonic measures are realized as weighted limits of large balls tangent to the leaves and that their conditional measures on the fibers are limits of weighted averages on the orbits of the holonomy group.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 4 , June 2018 , pp. 1238 - 1288
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, J., Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140 (2000), 351–398.Google Scholar
Alvarez, S.. Discretization of harmonic measures for foliated bundles. C. R. Acad. Sci. Paris Ser. I 350 (2012), 621–626.CrossRefGoogle Scholar
Alvarez, S.. Harmonic measures and the foliated geodesic flow for foliations with negatively curved leaves. Ergod. Th. & Dynam. Sys. 36 (2016), 355–374.Google Scholar
Alvarez, S.. Gibbs u-states for the foliated geodesic flow and transverse invariant measures. Preprint, 2013, arXiv:1311.7121.Google Scholar
Alvarez, S.. A Fatou theorem for $F$ -harmonic functions. Math. Z., accepted, doi:10.1007/s00209-016-1819-2. Preprint, 2015, arXiv:1512.01842.CrossRefGoogle Scholar
Alvarez, S.. Mesures de Gibbs et mesures harmoniques pour les feuilletages aux feuilles courbées négativement. Thèse, l’Université de Bourgogne, 2013.Google Scholar
Anosov, D.. Geodesic flows on closed Riemannian manifolds with negative curvature. Proc. Steklov Inst. Math. A.M.S. Transl. 90 (1969), iv+235pp.Google Scholar
Alcalde Cuesta, F. and Rechtman, A.. Averaging sequences. Pacific J. Math. 255 (2012), 1–23.CrossRefGoogle Scholar
Anderson, M. T. and Schoen, R.. Positive harmonic functions on complete manifolds of negative curvature. Ann. of Math. (2) 121 (1985), 429–461.Google Scholar
Alvarez, S. and Yang, J.. Physical measures for the geodesic flow tangent to a transversally conformal foliation. Preprint, 2015, arXiv:1512.01842.Google Scholar
Babillot, M.. On the mixing property for hyperbolic systems. Israel J. Math. 129 (2002), 61–76.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective (Encyclopaedia of Mathematical Sciences, 102. Mathematical Physics, III) . Springer, Berlin, 2005.Google Scholar
Bers, L.. Simultaneous uniformization. Bull. Amer. Math. Soc. (N.S.) 66 (1960), 94–97.CrossRefGoogle Scholar
Bonatti, C. and Gómez-Mont, X.. Sur le comportement statistique des feuilles de certains feuilletages holomorphes. Monogr. Enseign. Math. 38 (2001), 15–41.Google Scholar
Bonatti, C., Gómez-Mont, X. and Martínez, M.. Foliated hyperbolicity and foliations with hyperbolic leaves. Preprint, 2015, arXiv:1510.05026.Google Scholar
Bonatti, C., Gómez-Mont, X. and Viana, M.. Généricité d’exposants de Lyapunov non-nuls pour des produits déterministes de matrices. Ann. Inst. H. Poincaré Anal. Non Linéaire 20 (2003), 579–624.CrossRefGoogle Scholar
Bonatti, C., Gómez-Mont, X. and Vila, R.. Statistical behaviour of the leaves of Riccati foliations. Ergod. Th. & Dynam. Sys. 30 (2010), 67–96.Google Scholar
Babillot, M. and Ledrappier, F.. Geodesic paths and horocycle flows on abelian covers. Lie Groups and Ergodic Theory (Mumbai, 1996) (Tata Institute of Fundamental Research Studies in Mathematics, 14) . Tata Institute of Fundamental Research, Bombay, 1998, pp. 1–32.Google Scholar
Bowen, R. and Marcus, B.. Unique ergodicity for horocycle foliations. Israel J. Math. 26 (1977), 43–67.CrossRefGoogle Scholar
Bakhtin, Y. and Martínez, M.. A characterization of harmonic measures on laminations by hyperbolic Riemann surfaces. Ann. Inst. Henri Poincaré Probab. Stat. 44 (2008), 1078–1089.Google Scholar
Bowen, R.. Symbolic dynamics for hyperbolic flows. Amer. J. Math. 95 (1973), 429–459.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470) . Springer, Berlin, 1975.Google Scholar
Bowen, R.. Hausdorff dimension of quasi-circles. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 259–273.CrossRefGoogle Scholar
Bowen, R. and Ruelle, D.. The ergodic theory of Axiom A flows. Invent. Math. 29 (1975), 181–202.Google Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115 (2000), 157–193.Google Scholar
Benedicks, M. and Young, L. S.. SRB-measures for certain Hénon maps. Invent. Math. 112 (1993), 541–576.Google Scholar
Carvalho, M.. Sinai–Ruelle–Bowen measures for n-dimensional derived from Anosov diffeomorphisms. Ergod. Th. & Dynam. Sys. 13 (1993), 21–44.Google Scholar
Camacho, C. and Neto, A. L.. Geometric Theory of Foliations. Birkhäuser, Boston, MA, 1985.Google Scholar
Deroin, B. and Kleptsyn, V.. Random conformal dynamical systems. Geom. Funct. Anal. 17 (2007), 1043–1105.Google Scholar
Garnett, L.. Foliations, the ergodic theorem and Brownian motion. J. Funct. Anal. 51 (1983), 285–311.Google Scholar
Ghys, E., Langevin, R. and Walczak, P.. Entropie géométrique des feuilletages. Acta Math. 160 (1988), 105–142.Google Scholar
Kaimanovich, V.. Invariant measures of the geodesic flow and measures at infinity on negatively curved manifolds. Ann. Inst. H. Poincaré Phys. Théor. 53 (1990), 361–393.Google Scholar
Kaimanovich, V.. Amenability, hyperfiniteness, and isoperimetric inequalities. C. R. Acad. Sci. Paris Ser. I 325 (1997), 999–1004.Google Scholar
Katok, A.. Entropy and closed geodesics. Ergod. Th. & Dynam. Sys. 2 (1982), 339–365.Google Scholar
Katok, A.. Four applications of conformal equivalence to geometry and dynamics. Ergod. Th. & Dynam. Sys. 8 (1988), 115–140.Google Scholar
Kaimanovich, V. and Lyubich, M.. Conformal and harmonic measures on laminations associated with rational maps. Mem. Amer. Math. Soc. 173 (2005), vi+119pp.Google Scholar
Knieper, G.. Spherical means on compact manifolds of negative curvature. J. Differential Geom. Appl. 4 (1994), 361–390.Google Scholar
Knieper, G. and Peyerimhoff, N.. Ergodic properties of isoperimetric domains in spheres. J. Mod. Dyn. 2 (2008), 239–358.Google Scholar
Ledrappier, F.. Ergodic properties of Brownian motion on covers of compact negatively curved manifolds. Bol. Soc. Bras. Mat. 19 (1988), 115–140.Google Scholar
Ledrappier, F.. Harmonic measures and Bowen–Margulis measures. Israel J. Math. 71 (1990), 275–287.Google Scholar
Ledrappier, F.. Structure au bord des variétés à courbure négative. Sémin. Théor. Spectrale Géom. 13 (1994–1995), 93–118.CrossRefGoogle Scholar
Ledrappier, F.. A renewal theorem for the distance in negative curvature. Proc. Sympos. Pure Math. 57 (1995), 351–360.Google Scholar
Martínez, M.. Measures on hyperbolic surface laminations. Ergod. Th. & Dynam. Sys. 26 (2006), 847–867.Google Scholar
Patterson, S. J.. The limit set of a Fuchsian group. Acta Math. 136 (1976), 241–273.Google Scholar
Paulin, F., Pollicott, M. and Schapira, B.. Equilibrium States in Negative Curvature (Astérisque, 373) . Société Mathématique de France, Paris, 2015.Google Scholar
Pesin, Y. and Sinai, Y.. Gibbs measures for partially hyperbolic attractors. Ergod. Th. & Dynam. Sys. 2 (1982), 417–438.Google Scholar
Ratner, M.. Markov partitions for Anosov flows on n-dimensional manifolds. Israel J. Math. 15 (1973), 92–114.CrossRefGoogle Scholar
Rokhlin, V. A.. On the fundamental ideas of measure theory. Amer. Math. Soc. Transl. 10 (1962), 1–52.Google Scholar
Roblin, T.. Ergodicité et équidistribution en courbure négative. Mém. Soc. Math. Fr. (N.S.) 95 (2003), vi+96pp.Google Scholar
Schapira, B.. On quasi-invariant transverse measures for the horospherical foliation of a negatively curved manifold. Ergod. Th. & Dynam. Sys. 24 (2004), 227–257.Google Scholar
Schapira, B.. Mesures quasi-invariantes pour un feuilletage et limites de moyennes longitudinales. C. R. Acad. Sci. Paris Ser. I 336 (2003), 349–352.CrossRefGoogle Scholar
Shub, M.. Stabilité globale des systèmes dynamiques (Astérisque, 56) . Société Mathématique de France, Paris, 1978.Google Scholar
Sinai, Y.. Gibbs measures in ergodic theory. Russian Math. Surveys 27 (1972), 21–69.Google Scholar
Thurston, W.. Geometry and topology of 3-Manifolds. Princeton Lecture Notes, 1980, currently available at library.msri.org/books/gt3m/.Google Scholar
Young, L. S.. Large deviations in dynamical systems. Trans. Amer. Math. Soc. 318 (1990), 525–543.Google Scholar