Hostname: page-component-6bf8c574d5-5ws7s Total loading time: 0 Render date: 2025-03-08T05:35:34.072Z Has data issue: false hasContentIssue false
  • English
  • Français

The geometric index and attractors of homeomorphisms of 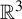$\mathbb {R}^3$

Part of: Homology and cohomology theories Low-dimensional dynamical systems Topological dynamics

Published online by Cambridge University Press:  18 October 2021

H. BARGE Open the ORCID record for H. BARGE [Opens in a new window]  and
J. J. SÁNCHEZ-GABITES
H. BARGE
Affiliation:
E.T.S. Ingenieros informáticos, Universidad Politécnica de Madrid, 28660 Madrid, España (e-mail: [email protected])
J. J. SÁNCHEZ-GABITES*
Affiliation:
Facultad de Ciencias Matemáticas, Universidad Complutense de Madrid, 28040 Madrid, España
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we focus on compacta 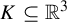$K \subseteq \mathbb {R}^3$ which possess a neighbourhood basis that consists of nested solid tori 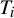$T_i$. We call these sets toroidal. Making use of the classical notion of the geometric index of a curve inside a torus, we introduce the self-geometric index of a toroidal set K, which roughly captures how each torus 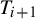$T_{i+1}$ winds inside the previous 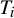$T_i$ as 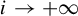$i \rightarrow +\infty $. We then use this index to obtain some results about the realizability of toroidal sets as attractors for homeomorphisms of 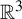$\mathbb {R}^3$.

Keywords

toroidal setgeometric indexattractor

MSC classification

Primary: 37B35: Gradient-like and recurrent behavior; isolated (locally maximal) invariant sets 37E99: None of the above, but in this section
Secondary: 55N99: None of the above, but in this section
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 1 , January 2023 , pp. 50 - 77
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrist, K. B., Garity, D. J., Repovš, D. and Wright, D. G.. New techniques for computing geometric index. Mediterr. J. Math. 14(6) (2017), Article no. 237, 15 pp.CrossRefGoogle Scholar
Barge, H. and Sánchez-Gabites, J. J.. Knots and solenoids that cannot be attractors of self-homeomorphisms of $\ {\mathbb{R}}^3$ . Int. Math. Res. Not. 13 (2021), 10373–10407.CrossRefGoogle Scholar
Bhatia, N. P. and Szegő, G. P.. Stability Theory of Dynamical Systems (Die Grundlehren der mathematischen Wissenschaften, 161). Springer, Berlin, 1970.CrossRefGoogle Scholar
Bing, R. H.. Locally tame sets are tame. Ann. Math. (2) 59(1) (1954), 145–158.Google Scholar
Burde, G. and Zieschang, H.. Knots (De Gruyter Studies in Mathematics, 5). Walter de Gruyter, Berlin, 2003.Google Scholar
Crovisier, S. and Rams, M.. IFS attractors and Cantor sets. Topol. Appl. 153 (2006), 1849–1859.CrossRefGoogle Scholar
Daverman, R. J. and Venema, G. A.. Embeddings in Manifolds. American Mathematical Society, Providence, RI, 2009.Google Scholar
Duvall, P. F. and Husch, L. S.. Attractors of iterated function systems. Proc. Amer. Math. Soc. 116 (1992), 279–284.CrossRefGoogle Scholar
Edwards, C. H.. Concentricity in $3$ -manifolds. Trans. Amer. Math. Soc. 113(3) (1964), 406–423.Google Scholar
Edwards, R. D.. The solution of the 4-dimensional annulus conjecture (after Frank Quinn). Four-Manifold Theory (Contemporary Mathematics, 35). Eds. Gordon, C. and Kirby, R.. American Mathematical Society, Providence, RI, 1984, pp. 211–264.CrossRefGoogle Scholar
Garay, B. M.. Strong cellularity and global asymptotic stability. Fund. Math. 138 (1991), 147–154.Google Scholar
Grayson, M. and Pugh, C.. Critical sets in 3-space. Publ. Math. Int. Hautes Études Sci. 77 (1993), 5–61.Google Scholar
Grines, V., Laudenbach, F. and Pochinka, O.. Self-indexing energy function for Morse–Smale diffeomorphisms on 3-manifolds. Mosc. Math. J. 9(4) (2009), 801–821.Google Scholar
Günther, B.. A compactum that cannot be an attractor of a self-map on a manifold. Proc. Amer. Math. Soc. 120(2) (1994), 653–655.Google Scholar
Günther, B. and Segal, J.. Every attractor of a flow on a manifold has the shape of a finite polyhedron. Proc. Amer. Math. Soc. 119(1) (1993), 321–329.Google Scholar
Hudson, J. F. P. and Zeeman, E. C.. On regular neighbourhoods. Proc. Lond. Math. Soc. 14(3) (1964), 719–745.CrossRefGoogle Scholar
Jiang, B., Ni, Y. and Wang, S.. 3-manifolds that admit knotted solenoids as attractors. Trans. Amer. Math. Soc. 356(11) (2004), 4371–4382.Google Scholar
Jiménez, V. and Llibre, J.. A topological characterization of the $\omega$ -limit sets for analytic flows on the plane, the sphere and the projective plane. Adv. Math. 216 (2007), 677–710.Google Scholar
Jiménez, V. and Peralta-Salas, D.. Global attractors of analytic plane flows. Ergod. Th. & Dynam. Sys. 29 (2009), 967–981.Google Scholar
Kato, H.. Attractors in Euclidean spaces and shift maps on polyhedra. Houston J. Math. 24 (1998), 671–680.Google Scholar
Lickorish, W. B. R.. An Introduction to Knot Theory (Graduate Texts in Mathematics, 175). Springer, New York, 1997.Google Scholar
McCord, M. C.. Inverse limit sequences with covering maps. Trans. Amer. Math. Soc. 114(1) (1965), 197–209.CrossRefGoogle Scholar
Moise, E. E.. Geometric Topology in Dimensions 2 and 3. Springer, New York, 1977.CrossRefGoogle Scholar
Norton, A. and Pugh, C.. Critical sets in the plane. Michigan Math. J. 38(3) (1991), 441–459.CrossRefGoogle Scholar
Ortega, R. and Sánchez-Gabites, J. J.. A homotopical property of attractors. Topol. Methods Nonlinear Anal. 46 (2015), 1089–1106.CrossRefGoogle Scholar
Rolfsen, D.. Knots and Links. AMS Chelsea Publishing, Providence, RI, 2003.Google Scholar
Rourke, C. P. and Sanderson, B. J.. Introduction to Piecewise-Linear Topology (Ergebnisse der Mathematik und ihrer Grenzgebiete, 69). Springer, Berlin, 1972.Google Scholar
Sánchez-Gabites, J. J.. How strange can an attractor for a dynamical system in a $3$ -manifold look? Nonlinear Anal. 74 (2011), 6162–6185.CrossRefGoogle Scholar
Sánchez-Gabites, J. J.. Arcs, balls and spheres that cannot be attractors in $\ {\mathbb{R}}^3$ . Trans. Amer. Math. Soc. 368(5) (2016), 3591–3627.Google Scholar
Sánchez-Gabites, J. J.. On the set of wild points of attracting surfaces in $\ {\mathbb{R}}^3$ . Adv. Math. 315 (2017), 246–284.Google Scholar
Sanjurjo, J. M. R.. Multihomotopy, Čech spaces of loops and shape groups. Proc. Lond. Math. Soc. (3) 69(2) (1994), 330–344.CrossRefGoogle Scholar
Schubert, H.. Knoten und Vollringe. Acta Math. 90 (1953), 131–286.Google Scholar
Souto, J.. A remark about critical sets in $\ {\mathbb{R}}^3$ . Rev. Mat. Iberoam. 35(2) (2019), 461–469.Google Scholar
Williams, R. F.. Expanding attractors. Publ. Math. Int. Hautes Études Sci. 43 (1974), 169–203.CrossRefGoogle Scholar